Difference between revisions of "Linkability Rules"
m (→Quick overview: fix formatting, wording) |
(various formatting, change _distance to _span in examples) |
||
| Line 1: | Line 1: | ||
==Quick overview== | ==Quick overview== | ||
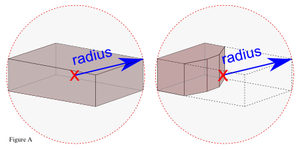
[[Image:Primitive_diameter.png|thumb|right|Figure A: The bounding spheres of two example prims, one of which has been cut. The two spheres are identical in size.]] | |||
* Whether two prims can be linked depends only on their scale and position. Other properties (such as rotation, hollow, cut, etc.) are ignored. This means that linking calculations are done as the prim were an undistorted rectangular box (with the same X, Y, and Z sizes, but everything else 'normal'). | * Whether two prims can be linked depends only on their scale and position. Other properties (such as rotation, hollow, cut, etc.) are ignored. This means that linking calculations are done as the prim were an undistorted rectangular box (with the same X, Y, and Z sizes, but everything else 'normal'). | ||
** Exception for megaprims: If any side is more than 10 meters, treat that side as if it were 10 meters. | ** Exception for megaprims: If any side is more than 10 meters, treat that side as if it were 10 meters. | ||
| Line 13: | Line 14: | ||
# Repeat with the new objects until you can't link in any more. | # Repeat with the new objects until you can't link in any more. | ||
Read the section below for details of the linkability formula, including examples and what actually gets linked when you can't | Read the section below for details of the linkability formula, including examples and what actually gets linked when you can't link everything. | ||
==The details== | ==The details== | ||
| Line 35: | Line 36: | ||
(7) A_can_link_to_B = ( length(center_A - center_B) + radius_A + radius_B <= max_link_span ) | (7) A_can_link_to_B = ( length(center_A - center_B) + radius_A + radius_B <= max_link_span ) | ||
The '''bounding sphere''' is the smallest sphere that totally encloses the | The '''bounding sphere''' is the smallest sphere that totally encloses the | ||
primitive's ''local bounding box''. | primitive's ''local bounding box''. | ||
| Line 107: | Line 105: | ||
2.06 is less than 54 | 2.06 is less than 54 | ||
Thus | Thus max_link_span = 2.06m | ||
==== one large prim and one small prim ==== | ==== one large prim and one small prim ==== | ||
| Line 122: | Line 120: | ||
16.03 is smaller than 54.0 | 16.03 is smaller than 54.0 | ||
Thus | Thus max_link_span = 16.03m | ||
==== 2 very large prims ==== | ==== 2 very large prims ==== | ||
| Line 128: | Line 126: | ||
thus, the diameter of a 10m x 10m x 10m prim is the square root of (100+100+100) = ~17.3m | thus, the diameter of a 10m x 10m x 10m prim is the square root of (100+100+100) = ~17.3m | ||
and the diameter of a 10m x 1m x 1m prim is square root (100+1+1) = ~10.1m | and the diameter of a 10m x 1m x 1m prim is square root (100+1+1) = ~10.1m | ||
(The type of prim doesn't matter for this calculation. We only care about the | (The type of prim doesn't matter for this calculation. We only care about the dimensions.) | ||
Let's take the case of two 10m x 10m x 10m prims. | Let's take the case of two 10m x 10m x 10m prims. | ||
| Line 143: | Line 141: | ||
53.96 is smaller than 54 | 53.96 is smaller than 54 | ||
Thus | Thus max_link_span = 53.96m | ||
[[Category:Havok4]] | [[Category:Havok4]] | ||
Revision as of 21:59, 1 April 2008
Quick overview
- Whether two prims can be linked depends only on their scale and position. Other properties (such as rotation, hollow, cut, etc.) are ignored. This means that linking calculations are done as the prim were an undistorted rectangular box (with the same X, Y, and Z sizes, but everything else 'normal').
- Exception for megaprims: If any side is more than 10 meters, treat that side as if it were 10 meters.
- At the small extreme: two tiny prims can be linked if they are within about 2 meters from each other.
- At the large extreme: the largest linked object that can be created must fit within a sphere with a diameter of 54 meters.
A layperson's explanation:
- Imagine transforming every prim in every object into the aforementioned boxes.
- For each existing (linked-together) object, imagine the smallest sphere that totally encloses the boxes that belong to it. (For individual prims, just enclose that one box.)
- Triple the size of each sphere, then add another meter around it. (Don't move the centers of the spheres.)
- For spheres that intersect, link those things into new objects.
- Exception: If any new object would need a sphere of bigger than 54 meters to enclose all its boxes, you can't make that object.
- Repeat with the new objects until you can't link in any more.
Read the section below for details of the linkability formula, including examples and what actually gets linked when you can't link everything.
The details
Consider two primitives, A and B. Whether they can be linked or not is determined by measuring the span from the edge of one object's bounding sphere to the far opposite edge of the other's bounding sphere and comparing that value to the maximum linkability span which is a function of the radii of the two bounding spheres:
(1) max_link_span = minimum( 3 * (radius_A + radius_B) + LINK_BONUS, LARGEST_MAX )
where:
(3) LINK_BONUS = 2.0 meters (4) LARGEST_MAX = 54.0 meters (5) radius_X = radius of the primitive X's bounding sphere (Figure A) (6) minimum(C, D) = C if less than D, otherwise D
If the measured span of the two bounding spheres is less than or equal to max_link_span then the corresponding primitives can be linked. Put in mathematical terms:
(7) A_can_link_to_B = ( length(center_A - center_B) + radius_A + radius_B <= max_link_span )
The bounding sphere is the smallest sphere that totally encloses the primitive's local bounding box.
The local bounding box is centered at the primitive's geometric center and has sides that are equal to the primitive's scale. One exception to this rule is that megaprim scale components greater than 10 meters are clamped to 10.
The geometric center of the primitive is its local symmetric center prior to any cut, shear, twist, taper, or hollow operations.
Note that a primitive's bounding sphere is not necessarily the tightest sphere possible for its shape, unless it is a simple box. The bounding sphere depends only on the primitive's position and scale, so any severly cut and hollowed primitive will be significantly smaller than its bounding sphere, and not necessarily near the center. Also, a primitive with twist and/or shear may have corners that extend outside of its bounding sphere. Since the linkability rules depend only on the bounding sphere, which is ultimately dependent only on the primitive's position and scale, the linkability of two prims is independent of changes to form and rotation.
TODO -- we need a new figure_A that shows radius instead of diameter. Also need new figures _B and _C for two linkable prims and two linkable multi-prim objects.
Linkability algorithm
The rules governing the linkability of multi-prim objects is very similar to the two-primitive case. The same formulae (1) and (7) apply, but the bounding spheres of multi-prim objects are the smallest spheres that completely contain all of the bounding spheres of the corresponding primitives.
When linking three or more objects the algorithm iterates over the candidate objects until all linkable pieces have been found. First the root object is tested against each candidate object and the larger bounding sphere is recomputed after a successful link. Then any unlinked pieces are tested between themselves and merged into larger collections according to the formulae. The root object is then re-tested against the modified candidates and the process continues until all objects are linked, or no new links have been found.
Failure modes
If an unlinkable set is tested by the linkability algorithm then the final subset of linkable parts is determined by the order in which the candidates were submitted. The trivial proof for this is to consider a root primitive in the middle of an infinite grid of other primitives. It can't link to everything, but it were first tested against all primitives west of it the final linkable subset of that first operation might not link to any primitives to the east because of the LARGEST_MAX requirement (4). If the primitives to the east were tested first then the final result would be different.
If a linkable set is tested by the linkability algorithm then the final subset of linkable parts is NOT affected by the order in which the candidates were submitted. That is, if just the linkable subsets of the failure modes above are tested for all permutations of sequence they will always link. The proof of this is left as an exercise for the reader.
Examples
2 very small prims
radius_A = ~0.01
radius_B = ~0.01
LINK_BONUS = 2.0 meters
LARGEST_MAX = 54.0 meters
3 * (radius_A + radius_B) + LINK_BONUS = 2.06 meters
2.06 is less than 54
Thus max_link_span = 2.06m
one large prim and one small prim
radius_A = 5m
radius_B = ~0.01
LINK_BONUS = 2.0 meters
LARGEST_MAX = 54.0 meters
3 * (radius_A + radius_B) + LINK_BONUS = 16.03 meters
16.03 is smaller than 54.0
Thus max_link_span = 16.03m
2 very large prims
The diameter of a bounding sphere is the square root of x^2 + y^2 + z^2 thus, the diameter of a 10m x 10m x 10m prim is the square root of (100+100+100) = ~17.3m and the diameter of a 10m x 1m x 1m prim is square root (100+1+1) = ~10.1m (The type of prim doesn't matter for this calculation. We only care about the dimensions.) Let's take the case of two 10m x 10m x 10m prims.
radius_A = 8.66m
radius_B = 8.66m
LINK_BONUS = 2.0 meters
LARGEST_MAX = 54.0 meters
3 * (radius_A + radius_B) + LINK_BONUS = 53.96m
53.96 is smaller than 54
Thus max_link_span = 53.96m