Difference between revisions of "Quaternion/fr"

From Second Life Wiki
Jump to navigation Jump to search
m (grrr)
m (help header)
 
(8 intermediate revisions by one other user not shown)
Line 1: Line 1:
{{LSL Header}}
{{Help/fr|Parent=Quaternion|Glossary=*}}
{{LSL Header/fr}}
==quaternion==
==quaternion==


Un mot-clé accepté par le compilateur qui signifie la même chose que {{LSLG|rotation/fr|rotation}} et est interchangeable avec lui.
Un mot-clé accepté par le compilateur, qui signifie la même chose que {{LSLG|rotation/fr|rotation}} et est interchangeable avec lui.


[[Category:LSL Types/fr|Quaternion/fr|Quaternion]]
[[Category:LSL Types/fr|Quaternion/fr|Quaternion]]
Line 8: Line 9:




== Definition and Properties: ==
== Définition et propriétés ==


Quaternions are a generalization of complex numbers, invented by William Rowan Hamilton in the mid-19th century.  Recall that a complex number is the sum of an ordinary real number a and an imaginary number bi, where i is defined by:
Les quaternions sont une généralisation des nombres complexes inventée par William Rowan Hamilton au milieu du 19ème siècle. Rappelez-vous qu'un nombre complexe est la somme d'un nombre réel ordinaire a et d'un nombre imaginaire bi, où i est défini par :


i<sup>2</sup> = -1
i<sup>2</sup> = -1


To construct a quaternion we introduce additional generalized imaginary units j and k with the assumptions:
Pour construire un quaternion, nous introduisons des unités imaginaires généralisées j et k avec les hypothèses :


j<sup>2</sup> = -1;    k<sup>2</sup> = -1;    ijk = -1
j<sup>2</sup> = -1 ;    k<sup>2</sup> = -1 ;    ijk = -1


From these basic definitions it is easy to derive the multiplication relations for these generalized imaginary quantities:
À  partir de ces définitions de base il est facile de dériver les relations multiplicatives entre ces quantités imaginaires généralisées :


ij = k;    jk = i;    ki = j
ij = k ;    jk = i ;    ki = j


and
et


ji = -k;    kj = -i;    ik = -j
ji = -k ;    kj = -i ;    ik = -j


That is, the multiplication of quaternions is not commutative.  While non-commutative operations are now a familiar feature of matrix algebra and vector and tensor analysis, at the time of their invention the idea was radical.   
Cela veut dire que la multiplication des quaternions n'est pas commutative.  Bien que les opérations non commutatives soient de nos jours une caractéristique familière de l'algèbre linéaire, à l'époque de leur invention l'idée était révolutionnaire.   


A quaternion is then a number of the form
Un quaternion est donc un nombre de la forme


Q = a + bi + cj + dk
Q = a + bi + cj + dk


where a,b, and c are ordinary real numbers. Adding quaternions is easy enough; one just adds the corresponding multipliers:
où a, b et c sont des nombres réels ordinaires. Ajouter des quaternions est assez facile, on ajoute simplement les facteurs correspondants :


a + bi + cj + dk + e + fi + gj + hk = ( a+e) + (b+f)i + (c+g)j + (d+h)k
a + bi + cj + dk + e + fi + gj + hk = ( a+e) + (b+f)i + (c+g)j + (d+h)k


The result of multiplying two quaternions can be worked out using the product relations above, remembering to preserve the order of terms in i,j,k since the imaginary units do not commute.   
Le résultat de la multiplication de deux quaternions peut être déduit des relations multiplicatives précédentes, en se souvenant de conserver l'ordre des termes en i, j et k puisque les unités imaginaires ne commutent pas.   


QR = (a + bi + cj + dk)(e + fi + gj + hk) =
QR = (a + bi + cj + dk)(e + fi + gj + hk) =
Line 53: Line 54:
= (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag -bh + ce + df)j + (ah + bg - cf + de)k
= (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag -bh + ce + df)j + (ah + bg - cf + de)k


(And you thought multiplying complex numbers was a mess!)
(... et vous qui pensiez que la multiplication des nombres complexes était compliquée !)


Now, we can define the analog of a complex conjugate (we'll use the * notation but other notations are also common):
À présent, nous pouvons définir l'équivalent du conjugué d'un nombre complexe (nous utiliserons la notation *, mais d'autres notations sont également répandues) :


Q*= a - bi - cj - dk
Q*= a - bi - cj - dk


The product of a quaternion and its conjugate is:
Le produit d'un quaternion et de son conjugué est :
                                          
                                          
QQ* = (a + bi + cj + dk)(a - bi - cj - dk) =
QQ* = (a + bi + cj + dk)(a - bi - cj - dk) =
Line 67: Line 68:
= (a<sup>2</sup> + b<sup>2</sup> + c<sup>2</sup> + d<sup>2</sup>)
= (a<sup>2</sup> + b<sup>2</sup> + c<sup>2</sup> + d<sup>2</sup>)


which looks rather like a Euclidean length. If we regard the triplet (b,c,d) as a vector V, we can rewrite this length as:
ce qui ressemble drôlement au carré d'une longueur euclidienne. Si nous considérons le triplet (b, c, d) comme un vecteur V, nous pouvons réécrire cette longueur au carré comme :


QQ* = a<sup>2</sup> + ||V||<sup>2</sup>
QQ* = a<sup>2</sup> + ||V||<sup>2</sup>


The first term, a, is thus often referred to as the scalar or sometimes the real part of the quaternion, and the triplet (b,c,d) as the vector part.
Le premier terme, a, est souvent désigné comme le scalaire, ou parfois comme la partie réelle du quaternion, et le triplet (b, c, d) comme la partie vectorielle.


== Quaternions and Rotations: ==
== Quaternions et rotations ==


The reason we care about quaternions is that Second Life uses them to represent rotations. How is this done?  Consider the quaternion representation of a vector V = (b,c,d), which is just a quaternion with a zero real part:
La raison qui nous fait nous intéresser aux quaternions est que Second Life les utilise pour représenter des rotations. Comment cela ?  Considerons la représentation sous forme de quaternion d'un vecteur V = (b, c, d), c'est-à-dire simplement un quaternion avec une partie réelle nulle :


Q(V) = 0 + bi + cj + dk
Q(V) = 0 + bi + cj + dk


If we multiply Q by some other quaternion, in general we will get a non-zero real part; that is, we've transformed the vector into a non-vector quaternion, which doesn't look at all like a rotation. However, if we multiply on one side by a quaternion z, and on the other side by the multiplicative inverse of z, z<sup>-1</sup>, we will get a result with a 0-value real part:
Si nous multiplions Q par un autre quaternion, en général nous obtenons une partie réelle non nulle ; en d'autres termes, nous avons transformé le vecteur en un quaternion qui n'est pas un vecteur, ce qui ne ressemble pas du tout à l'effet attendu d'une rotation. Néanmoins, si nous multiplions d'un côté par un quaternion z, et de l'autre côté par l'inverse pour la multiplication de z, z<sup>-1</sup>, nous obtenons un résultat avec une partie réelle nulle :


Re[zQ(V)z<sup>-1</sup>]  = 0
Re[zQ(V)z<sup>-1</sup>]  = 0


-- that is, we'll map a vector into a vector.  To see that this is so, note that from the formula for multiplication, the real part of the product of two quaternions is invariant to the order of multiplication, that is:
-- en fait, nous avons transformé un vecteur en vecteur. Pour s'assurer qu'il en est bien ainsi, on remarque que dans les formules de multiplication, la partie réelle de deux quaternions ne dépend pas de l'ordre de multiplication, c'est-à-dire :


Re[QR] = Re[RQ].
Re[QR] = Re[RQ].


So we can invert the order of the first and (second*third) quaternions in the mapping without changing the real part:
Nous pouvons donc inverser l'ordre du premier et du troisième quaternions dans la transformation sans changer la partie réelle :


Re[z(Q(V)z<sup>-1</sup>)]  = Re[(Q(V)z<sup>-1</sup>)z]  = Re[Q(V)(z<sup>-1</sup>z)]  =  Re[Q(V)(1)]  = 0
Re[z(Q(V)z<sup>-1</sup>)]  = Re[(Q(V)z<sup>-1</sup>)z]  = Re[Q(V)(z<sup>-1</sup>z)]  =  Re[Q(V)(1)]  = 0


since quaternion multiplication is associative and we assumed that Q has a zero-value real part. This operation of left-multiplying by a quaternion and right-multiplying by its inverse is known as conjugation by z. Readers familiar with matrix algebra will recognize it as similar to the decomposition of a matrix into a rotation and a pure scaling (a diagonal matrix).   
puisque la multiplication des quaternions est associative et que nous avions supposé que Q a une partie réelle nulle. Cette opération consistant à multiplier à gauche par un quaternion et à droite par son inverse est connue sous le nom de conjugaison par z. Les lecteurs familiers avec le calcul matriciel verront la ressemblance avec la décomposition d'une matrice en une rotation et un pur changement d'échelle (une matrice diagonale).   


Under what conditions does conjugation of a quaternion give back the original quaternion?
À quelle condition le conjugué d'un quaternion est-il identique au quaternion de départ ?


zQz<sup>-1</sup> = Q implies  zQ = Qz
zQz<sup>-1</sup> = Q   implique    zQ = Qz


(which can be easily shown by right-multiplying the first expression by z). When do quaternions commute? From the expression for the product of two quaternions, recalling that the real parts commute in general, we have for example for the part multiplying i:
(ce que l'on peut démontrer facilement en multipliant la première expression à droite par z). Quand les quaternions commutent-ils ? Si l'on revient à l'expression du produit de deux quaternions, en se souvenant que les parties réelles commutent de toute façon, nous avons par exemple pour la partie facteur de i :


(af + be + ch - dg)i + ... =  (eb+ fa + gd - hc)i + ...
(af + be + ch - dg)i + ... =  (eb+ fa + gd - hc)i + ...


in the case where multiplication is commutative. This can only be true if ch - dg = 0 or c/d = g/h: that is, the slope of the vector part in the (j,k) plane is the same for both quaternions. Since there's nothing special about i, this must also be true of the (i,j) and (i,k) planes: that is, the two quaternions must have vectors that point in the same direction.  Q and R must have vector parts that are collinear. It's not too hard to show that conjugation is also linear (that is, the conjugate of the sum is the sum of the conjugates), and it's easy to see that the length of the vector part of Q is preserved under conjugation.  What sort of length-conserving linear transformation preserves a vector only when its axis coincides with the vector?  Why -- a rotation, of course.  So conjugation of Q by z is equivalent to rotating the vector part of Q around the axis defined by the vector part of z. 
lorsque la multiplication est commutative. Cela ne peut être vrai que si ch - dg = 0, soit c/d = g/h : dans le cas où la pente de la partie vectorielle dans le plan (j, k) est la même pour les deux quaternions. En reprenant le même raisonnement pour les parties facteur de j et de k, il doit également en être de même dans les plans (i, j) et (i, k) : les deux quaternions doivent avoir des vecteurs qui pointent dans la même direction.  Q et R doivent avoir des parties vectorielles colinéaires.


Let's try a simple case. Consider the vector V = (1,0,0) and corresponding quaternion Q = 0 + i.  To rotate around the z-axis we need a quaternion z of the form a + ck.  The conjugation is then:
Il n'est pas dur non plus de voir que la conjugaison est également linéaire (que le conjugué d'une somme est égal à la somme des conjugués), et il est facile de voir que la longueur de la partie vectorielle de Q est préservée par conjuguaison. Quelle sorte de transformation conservant la longueur ne préserve un vecteur que lorsque son axe coincide avec le vecteur ? Mais -- une rotation, bien sûr. Ainsi, conjuguer Q par z revient à tourner la partie vectorielle de Q autour de l'axe défini par la partie vectorielle de z.   


Q' = (a+c k)(i)(a + ck)<sup>-1</sup>
Essayons sur un cas simple. Considérons le vecteur V = (1, 0, 0) et le quaternion correspondant Q = 0 + i. Pour tourner autour de l'axe des z, nous avons besoin d'un quaternion de la forme a + ck. Le conjugué est alors :


What is the inverse of z? It's easy to see that if we choose a and c so that the length of the quaternion is 1, then the inverse is equal to the conjugate:
Q' = (a+ck) (i) (a + ck)<sup>-1</sup>


len(z) = 1 = zz*  implies  z* = z<sup>-1</sup> 
Quel est l'inverse de z ? Il est facile de voir que si nous choisissons a et c de manière à ce que la longueur du quaternion soit 1, alors l'inverse est égal au conjugué :


so we can write:
longueur(z) = 1 = zz*  implique  z* = z<sup>-1</sup>


Q' = (a+c k)(i)(a - ck) = (a+c k)(ai  + cj) = a<sup>2</sup>i + acj + caj - c<sup>2</sup>i  = ( a<sup>2</sup>- c<sup>2</sup>)i + 2acj
ainsi nous pouvons écrire :


Q' = (a+ck) (i) (a - ck) = (a+ck) (ai  + cj) = a<sup>2</sup>i + acj + caj - c<sup>2</sup>i  = ( a<sup>2</sup>- c<sup>2</sup>)i + 2acj


with the constraint:
 
La contrainte :


a<sup>2</sup>+ c<sup>2</sup>  = 1   
a<sup>2</sup>+ c<sup>2</sup>  = 1   


implying that we can write  a = cos(θ/2), b = sin(θ/2)  for some angle θ  (the reason for the factor of 1/2 will become clear in a moment).
implique que nous pouvons écrire a = cos(θ/2), b = sin(θ/2)  pour un certain angle θ  (la raison d'être du facteur 1/2 deviendra claire dans un moment).


Now, the terms in i and j become respectively:
Les termes en i et j deviennent respectivement :


cos<sup>2</sup>(θ/2) - sin<sup>2</sup>(θ/2) = cos(θ)
cos<sup>2</sup>(θ/2) - sin<sup>2</sup>(θ/2) = cos(θ)


and
et


2 cos(θ/2) sin(θ/2) = sin(θ)
2 cos(θ/2) sin(θ/2) = sin(θ)




So this indeed represents a rotation of the i (x) axis by the angle θ. We can infer that in the general case, to rotate a vector V around an axis A= (b,c,d)  (presumed normalized, that is ||A|| = 1) by an angle θ, we construct the quaternion
Cela représente bien une rotation de i d'un angle θ. Nous pouvons généraliser cela, pour tourner un vecteur V autour d'un axe porté par un vecteur unitaire A= (b, c, d)  (||A|| = 1) d'un angle θ, nous construisons le quaternion


z = cos(θ/2) + sin(θ/2)A = cos(θ/2) + sin(θ/2){bi + cj + dk}
z = cos(θ/2) + sin(θ/2)A = cos(θ/2) + sin(θ/2){bi + cj + dk}


and then conjugate the quaternion Q = 0 + V with z :
et nous conjuguons ensuite le quaternion Q = 0 + V par z :


Q' = zQz*
Q' = zQz*


from which we extract the vector part:
duquel nous extrayons la partie vectorielle :
 
Q' = 0 + V' => V'


Q' = 0 + V' => V' being the rotated vector V.   
V' étant le vecteur V après rotation.   




In Second Life, quaternions representing rotations are given as four real numbers. The first three are the vector part, and the last is the scalar part:  Q = (Q.x, Q.y, Q.z, Q.s). In terms of Second Life region directions, the East-West direction is the x-axis, the North-South direction is the y-axis, and the Up-Down direction is the z-axis.  Recall that x maps to the imaginary i axis, y to j, and to z to k. We can see that this is a right-handed coordinate system: if you wrap the fingers of your right hand from x to y, your thumb will point in the z direction. Default angles of rotation are defined in radians, from -π to π; that is, we can rotate counter-clockwise (in the positive direction) half-way around, or in the clockwise (negative) direction half-way around, with the two directions giving the same physical result at a rotation angle of 3.141 radians or 180 degrees. Thus a counter-clockwise rotation of a face pointing West, around the z axis by 90 degrees (to point South) is:
Dans Second Life, les quaternions qui représentent des rotations sont donnés sous la forme de quatre nombres en virgule flottante. Les trois premiers forment la partie vectorielle et le dernier est la partie scalaire :  Q = <Q.x, Q.y, Q.z, Q.s>. En termes de directions de régions de Second Life, la direction Est-Ouest est l'axe des x, la direction Nord-Sud est l'axe des y et la direction haut-bas est l'axe des z. Souvenez-vous que x correspond à l'axe imaginaire i, y à j et z à k. Nous pouvons voir qu'il s'agit d'un système de coordonnées direct, où s'applique donc la règle de la main droite : si vous enroulez les doigts de votre main droite de x vers y, votre pouce pointera dans la direction z. Par défaut, les angles de rotation sont définis en radians de -π à π ; nous pouvons donc tourner dans le sens contraire aux aiguilles d'une montre (sens positif) d'un demi-tour, ou dans le sens des aiguilles d'une montre (négatif) d'un demi-tour, en se retrouvant dans la même direction à un angle de rotation de 3,141 radians, soit 180 degrés. La rotation dans le sens contraire aux aiguilles d'une montre d'une face dirigée vers l'Ouest, autour de l'axe des z, de 90 degrés (pour se retrouver face au Sud) est :


(0,0,0.707,0.707)
<0, 0, 0.707, 0.707>


since the sine and cosine of π/4 (half of the rotation angle) are both 1/2<sup>0.5</sup>.   
puisque le sinus et le cosinus de π/4 (de la moitié de l'angle de rotation) valent tous les deux 1/2<sup>0.5</sup>.   




[[Image:example_rotation.jpg]]
[[Image:example_rotation_fr.jpg]]




Continuing around to point East is either
Pour continuer et pointer vers l'Est est soit


(0,0,1,0) or (0,0,-1,0)
<0, 0, 1, 0> soit <0, 0, -1, 0>


Tilting an object to the right (that is, rotating it counter-clockwise around the x-axis) by e.g. 90 degrees is described by:
Pour faire basculer (c'est-à-dire le faire tourner dans le sens contraire aux aiguilles d'une montre autour de l'axe des x) de 90 degrés est décrit par :


(0.707,0,0,0.707)
<0.707, 0, 0, 0.707>


and pitching forward (clockwise around the y-axis) by the same amount is
et pour le coucher (dans le sens des aiguilles d'une montre autour de l'axe des y) avec la même amplitude :


(0,-0.707,0,0.707).
<0, -0.707, 0, 0.707>.


It's important to note that the mapping of a single vector does not uniquely specify the corresponding quaternion rotation. For example, in the figure below we see a number of ways to rotate the x axis into the y axis. Different rotations result in different final orientations of the orthogonal (y and z) directions.   
Il est important de remarquer que la transformation d'un vecteur isolé ne détermine pas de façon unique la rotation à base de quaternion correspondante. Par exemple, dans la figure ci-dessous, nous voyons plusieurs façons de faire tourner l'axe des x jusqu'à ce qu'il coïncide avec l'axe des y. Des rotations différentes se traduisent par des orientations finales différentes dans les directions orthogonales (y et z).   




[[Image:Alternate_rotations.jpg]]
[[Image:Alternate_rotations_fr.jpg]]

Latest revision as of 16:56, 29 September 2008

quaternion

Un mot-clé accepté par le compilateur, qui signifie la même chose que rotation et est interchangeable avec lui.


Définition et propriétés

Les quaternions sont une généralisation des nombres complexes inventée par William Rowan Hamilton au milieu du 19ème siècle. Rappelez-vous qu'un nombre complexe est la somme d'un nombre réel ordinaire a et d'un nombre imaginaire bi, où i est défini par :

i2 = -1

Pour construire un quaternion, nous introduisons des unités imaginaires généralisées j et k avec les hypothèses :

j2 = -1 ; k2 = -1 ; ijk = -1

À partir de ces définitions de base il est facile de dériver les relations multiplicatives entre ces quantités imaginaires généralisées :

ij = k ; jk = i ; ki = j

et

ji = -k ; kj = -i ; ik = -j

Cela veut dire que la multiplication des quaternions n'est pas commutative. Bien que les opérations non commutatives soient de nos jours une caractéristique familière de l'algèbre linéaire, à l'époque de leur invention l'idée était révolutionnaire.

Un quaternion est donc un nombre de la forme

Q = a + bi + cj + dk

où a, b et c sont des nombres réels ordinaires. Ajouter des quaternions est assez facile, on ajoute simplement les facteurs correspondants :

a + bi + cj + dk + e + fi + gj + hk = ( a+e) + (b+f)i + (c+g)j + (d+h)k

Le résultat de la multiplication de deux quaternions peut être déduit des relations multiplicatives précédentes, en se souvenant de conserver l'ordre des termes en i, j et k puisque les unités imaginaires ne commutent pas.

QR = (a + bi + cj + dk)(e + fi + gj + hk) =

ae + afi + agj + ahk + bei - bf + bgij + bhik + cej + cfji - cg + chjk + dek + dfki + dgkj - dh

= ae + afi + agj + ahk + bei - bf + bgk - bhj + cej - cfk - cg + chi + dek + dfj - dgi - dh

= (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag -bh + ce + df)j + (ah + bg - cf + de)k

(... et vous qui pensiez que la multiplication des nombres complexes était compliquée !)

À présent, nous pouvons définir l'équivalent du conjugué d'un nombre complexe (nous utiliserons la notation *, mais d'autres notations sont également répandues) :

Q*= a - bi - cj - dk

Le produit d'un quaternion et de son conjugué est :

QQ* = (a + bi + cj + dk)(a - bi - cj - dk) =

= (a2 + b2 + c2 + d2) + (-ab + ba - cd + dc)i + (-ac + bd + ca - db)j + (-ad - bc + cb + da)k

= (a2 + b2 + c2 + d2)

ce qui ressemble drôlement au carré d'une longueur euclidienne. Si nous considérons le triplet (b, c, d) comme un vecteur V, nous pouvons réécrire cette longueur au carré comme :

QQ* = a2 + ||V||2

Le premier terme, a, est souvent désigné comme le scalaire, ou parfois comme la partie réelle du quaternion, et le triplet (b, c, d) comme la partie vectorielle.

Quaternions et rotations

La raison qui nous fait nous intéresser aux quaternions est que Second Life les utilise pour représenter des rotations. Comment cela ? Considerons la représentation sous forme de quaternion d'un vecteur V = (b, c, d), c'est-à-dire simplement un quaternion avec une partie réelle nulle :

Q(V) = 0 + bi + cj + dk

Si nous multiplions Q par un autre quaternion, en général nous obtenons une partie réelle non nulle ; en d'autres termes, nous avons transformé le vecteur en un quaternion qui n'est pas un vecteur, ce qui ne ressemble pas du tout à l'effet attendu d'une rotation. Néanmoins, si nous multiplions d'un côté par un quaternion z, et de l'autre côté par l'inverse pour la multiplication de z, z-1, nous obtenons un résultat avec une partie réelle nulle :

Re[zQ(V)z-1] = 0

-- en fait, nous avons transformé un vecteur en vecteur. Pour s'assurer qu'il en est bien ainsi, on remarque que dans les formules de multiplication, la partie réelle de deux quaternions ne dépend pas de l'ordre de multiplication, c'est-à-dire :

Re[QR] = Re[RQ].

Nous pouvons donc inverser l'ordre du premier et du troisième quaternions dans la transformation sans changer la partie réelle :

Re[z(Q(V)z-1)] = Re[(Q(V)z-1)z] = Re[Q(V)(z-1z)] = Re[Q(V)(1)] = 0

puisque la multiplication des quaternions est associative et que nous avions supposé que Q a une partie réelle nulle. Cette opération consistant à multiplier à gauche par un quaternion et à droite par son inverse est connue sous le nom de conjugaison par z. Les lecteurs familiers avec le calcul matriciel verront la ressemblance avec la décomposition d'une matrice en une rotation et un pur changement d'échelle (une matrice diagonale).

À quelle condition le conjugué d'un quaternion est-il identique au quaternion de départ ?

zQz-1 = Q implique zQ = Qz

(ce que l'on peut démontrer facilement en multipliant la première expression à droite par z). Quand les quaternions commutent-ils ? Si l'on revient à l'expression du produit de deux quaternions, en se souvenant que les parties réelles commutent de toute façon, nous avons par exemple pour la partie facteur de i :

(af + be + ch - dg)i + ... = (eb+ fa + gd - hc)i + ...

lorsque la multiplication est commutative. Cela ne peut être vrai que si ch - dg = 0, soit c/d = g/h : dans le cas où la pente de la partie vectorielle dans le plan (j, k) est la même pour les deux quaternions. En reprenant le même raisonnement pour les parties facteur de j et de k, il doit également en être de même dans les plans (i, j) et (i, k) : les deux quaternions doivent avoir des vecteurs qui pointent dans la même direction. Q et R doivent avoir des parties vectorielles colinéaires.

Il n'est pas dur non plus de voir que la conjugaison est également linéaire (que le conjugué d'une somme est égal à la somme des conjugués), et il est facile de voir que la longueur de la partie vectorielle de Q est préservée par conjuguaison. Quelle sorte de transformation conservant la longueur ne préserve un vecteur que lorsque son axe coincide avec le vecteur ? Mais -- une rotation, bien sûr. Ainsi, conjuguer Q par z revient à tourner la partie vectorielle de Q autour de l'axe défini par la partie vectorielle de z.

Essayons sur un cas simple. Considérons le vecteur V = (1, 0, 0) et le quaternion correspondant Q = 0 + i. Pour tourner autour de l'axe des z, nous avons besoin d'un quaternion de la forme a + ck. Le conjugué est alors :

Q' = (a+ck) (i) (a + ck)-1

Quel est l'inverse de z ? Il est facile de voir que si nous choisissons a et c de manière à ce que la longueur du quaternion soit 1, alors l'inverse est égal au conjugué :

longueur(z) = 1 = zz* implique z* = z-1

ainsi nous pouvons écrire :

Q' = (a+ck) (i) (a - ck) = (a+ck) (ai + cj) = a2i + acj + caj - c2i = ( a2- c2)i + 2acj


La contrainte :

a2+ c2 = 1

implique que nous pouvons écrire a = cos(θ/2), b = sin(θ/2) pour un certain angle θ (la raison d'être du facteur 1/2 deviendra claire dans un moment).

Les termes en i et j deviennent respectivement :

cos2(θ/2) - sin2(θ/2) = cos(θ)

et

2 cos(θ/2) sin(θ/2) = sin(θ)


Cela représente bien une rotation de i d'un angle θ. Nous pouvons généraliser cela, pour tourner un vecteur V autour d'un axe porté par un vecteur unitaire A= (b, c, d) (||A|| = 1) d'un angle θ, nous construisons le quaternion

z = cos(θ/2) + sin(θ/2)A = cos(θ/2) + sin(θ/2){bi + cj + dk}

et nous conjuguons ensuite le quaternion Q = 0 + V par z :

Q' = zQz*

duquel nous extrayons la partie vectorielle :

Q' = 0 + V' => V'

V' étant le vecteur V après rotation.


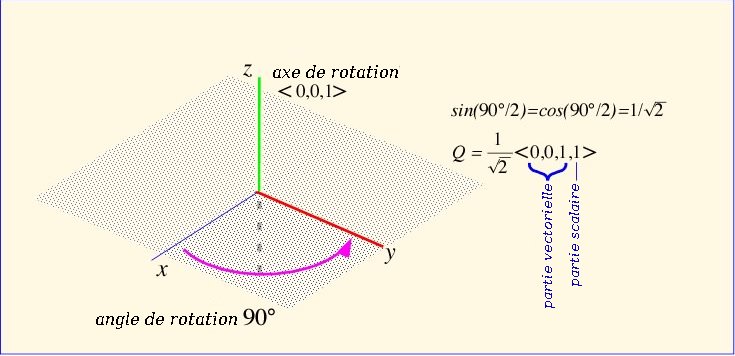
Dans Second Life, les quaternions qui représentent des rotations sont donnés sous la forme de quatre nombres en virgule flottante. Les trois premiers forment la partie vectorielle et le dernier est la partie scalaire : Q = <Q.x, Q.y, Q.z, Q.s>. En termes de directions de régions de Second Life, la direction Est-Ouest est l'axe des x, la direction Nord-Sud est l'axe des y et la direction haut-bas est l'axe des z. Souvenez-vous que x correspond à l'axe imaginaire i, y à j et z à k. Nous pouvons voir qu'il s'agit d'un système de coordonnées direct, où s'applique donc la règle de la main droite : si vous enroulez les doigts de votre main droite de x vers y, votre pouce pointera dans la direction z. Par défaut, les angles de rotation sont définis en radians de -π à π ; nous pouvons donc tourner dans le sens contraire aux aiguilles d'une montre (sens positif) d'un demi-tour, ou dans le sens des aiguilles d'une montre (négatif) d'un demi-tour, en se retrouvant dans la même direction à un angle de rotation de 3,141 radians, soit 180 degrés. La rotation dans le sens contraire aux aiguilles d'une montre d'une face dirigée vers l'Ouest, autour de l'axe des z, de 90 degrés (pour se retrouver face au Sud) est :

<0, 0, 0.707, 0.707>

puisque le sinus et le cosinus de π/4 (de la moitié de l'angle de rotation) valent tous les deux 1/20.5.


Example rotation fr.jpg


Pour continuer et pointer vers l'Est est soit

<0, 0, 1, 0> soit <0, 0, -1, 0>

Pour faire basculer (c'est-à-dire le faire tourner dans le sens contraire aux aiguilles d'une montre autour de l'axe des x) de 90 degrés est décrit par :

<0.707, 0, 0, 0.707>

et pour le coucher (dans le sens des aiguilles d'une montre autour de l'axe des y) avec la même amplitude :

<0, -0.707, 0, 0.707>.

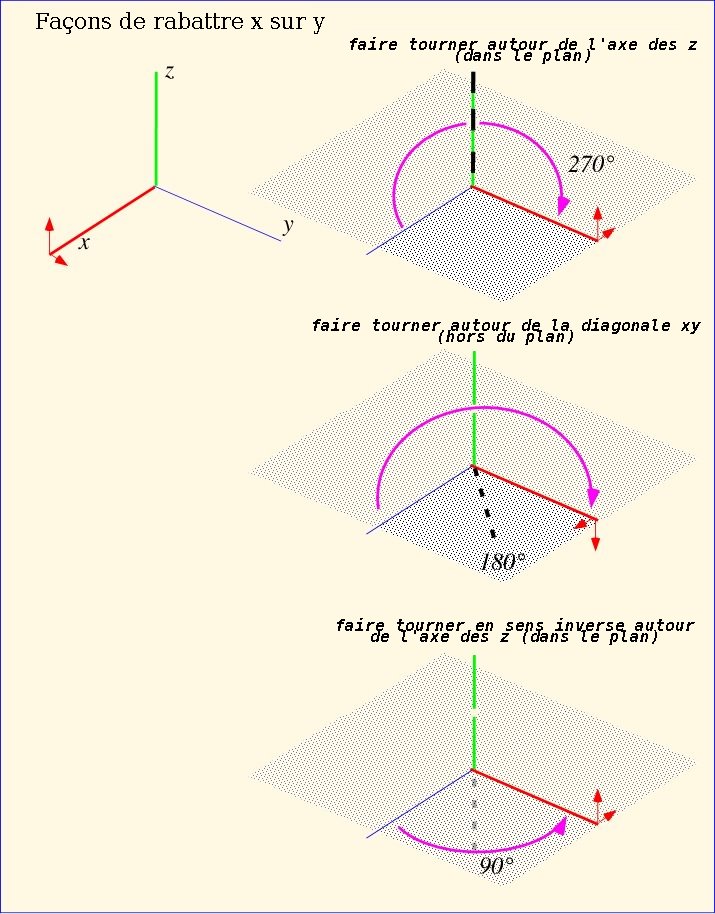
Il est important de remarquer que la transformation d'un vecteur isolé ne détermine pas de façon unique la rotation à base de quaternion correspondante. Par exemple, dans la figure ci-dessous, nous voyons plusieurs façons de faire tourner l'axe des x jusqu'à ce qu'il coïncide avec l'axe des y. Des rotations différentes se traduisent par des orientations finales différentes dans les directions orthogonales (y et z).


Alternate rotations fr.jpg

Retrieved from "https://wiki.secondlife.com/w/index.php?title=Quaternion/fr&oldid=93777"