Difference between revisions of "クォータニオン"
Naoya Bellic (talk | contribs) m |
Naoya Bellic (talk | contribs) m (英語版の変更に伴った変更) |
||
| Line 4: | Line 4: | ||
==クォータニオン== | ==クォータニオン== | ||
<code>クォータニオン</code>はLSLのコンパイラで回転を表現するものとして定義されており、<code>{{LSLG/ja|rotation}}</code>と言い換えることもできます。 | |||
Latest revision as of 15:14, 22 February 2013
| LSL ポータル | 関数 | イベント | 型 | 演算子 | 定数 | 実行制御 | スクリプトライブラリ | カテゴリ別スクリプトライブラリ | チュートリアル |
クォータニオン
クォータニオンはLSLのコンパイラで回転を表現するものとして定義されており、rotationと言い換えることもできます。
定義と詳細:
クォータニオンは複素数を一般化したもので、19世紀半ばにウィリアム・ローワン・ハミルトンによって考案されました。複素数は実数 a と純虚数 bi の和です。i は次のように定義されます。
i2 = -1
四元数を構築するため、次の仮定のもとに一般的な虚数単位 j と k を導入します。
j2 = -1; k2 = -1; ijk = -1
これらの基礎的な定義から、一般化された虚数単位の積についての関係を導くことができます。
ij = k; jk = i; ki = j
さらに、
ji = -k; kj = -i; ik = -j
つまり、クォータニオンの乗算は交換可能ではありません。交換可能でない演算は今でこそ行列代数やベクトルおよびテンソル解析でよく知られている特徴ですが、発明当時、この考え方は革命的でした。
クォータニオンの一般的な形は
Q = a + bi + cj + dk
ここで a、b、c は通常の実数です。クォータニオンの加算は簡単で、同類項をまとめるだけです。
(a + bi + cj + dk) + (e + fi + gj + hk) = (a+e) + (b+f)i + (c+g)j + (d+h)k
2つのクォータニオンの積は上述の積の関係を用いて求めることができます。虚数単位は交換可能でないので i、j、k の順序はそのままにしておきましょう。
QR = (a + bi + cj + dk)(e + fi + gj + hk) =
ae + afi + agj + ahk + bei - bf + bgij + bhik + cej + cfji - cg + chjk + dek + dfki + dgkj - dh
= ae + afi + agj + ahk + bei - bf + bgk - bhj + cej - cfk - cg + chi + dek + dfj - dgi - dh
= (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag - bh + ce + df)j + (ah + bg - cf + de)k
(そして、あなたは複素数の乗算は面倒だと思うでしょう!)
今、私たちは相似な共役複素数を定義することができます。(*表記を使用しますが、他の表記も一般的です)
Q* = a - bi - cj - dk
クォータニオンと、その共役複素数の積は:
QQ* = (a + bi + cj + dk)(a - bi - cj - dk) =
= (a2 + b2 + c2 + d2) + (-ab + ba - cd + dc)i + (-ac + bd + ca - db)j + (-ad - bc + cb + da)k
= (a2 + b2 + c2 + d2)
これはユークリッドノルムの2乗のように見えます。3つの組(b、c、d)をベクトル V とすると、この2乗されたノルムは書き直すことができ、
QQ* = a2 + ||V||2
なので、1つ目の項 a はクォータニオンのスカラー部または実部、3つの組(b、c、d)はベクトル部と呼ばれます。
クォータニオンと回転:
私たちがクォータニオンに関心がある理由は、Second Life が回転を表わすために使用しているからです。どのように行われているのでしょうか? 具体的にベクトル V = (b,c,d)、実部がゼロのクォータニオンで考えてみましょう。
Q(V) = 0 + bi + cj + dk
他のクォータニオンをQを掛けた場合、一般的に実部はゼロではありません。私たちはベクトルをベクトルではないクォータニオンに変換しました。回転にはとても見えませんね。でも、片方からあるクォータニオン z を掛け、その反対から z の逆数 z-1 を掛けると、実部がゼロの結果を得ることができます。
Re[zQ(V)z-1] = 0
-- すなわちベクトルからベクトルへの写像です。このことを確認するには、積の計算式から、2つのクォータニオンの積の実部は乗算の順序に対して不変であることに注目して、
Re[QR] = Re[RQ].
したがって、写像中の1番目と(2番目*3番目)のクォータニオンについて、実部を変えることなく順序を変えることができます。
Re[z(Q(V)z-1)] = Re[(Q(V)z-1)z] = Re[Q(V)(z-1z)] = 0
よって Q の実部がゼロのとき、クォータニオンの乗算でも結合法則を満たすことが分かりました。あるクォータニオンを左から掛け、さらに右からその逆数を掛けることは、z とその共役複素数を掛けるこの演算ですよね。線形代数に詳しい読者は、回転行列による対角化に似ていることに気付くのではないでしょうか。
では、あるクォータニオンとその共役なクォータニオンを掛けた結果、元のクォータニオンに戻るための条件は何でしょうか?
zQz-1 = Q ゆえに zQ = Qz
(これは最初の式の両辺に右から z を掛けることで簡単に示せます。) いつの間にクォータニオンが交換可能になったのでしょう? クォータニオンの積の式から、実部は交換可能であることが分かっていて、i の項については、
(af + be + ch - dg)i + ... = (eb + fa + gd - hc)i + ...
この乗算は ch - dg = 0 または c/d = g/h のとき交換可能です。すなわち、両方のクォータニオンのベクトル部のjk-平面における勾配が一致するときです。何も i が特別なわけではなく、ij-平面、ik-平面についても同様です。つまり2つのクォータニオンのベクトル部が同じ向き、言い換えると同一直線上にあるときに交換可能です。
このことを示すのは難しくなく、共役複素数は線形で(合計してから複素共役を取っても、複素共役を取ってから合計しても同じです)、共役を取っても Q のベクトル部の大きさは変わらないことは明らかです。軸がベクトルと一致する場合に限り、ベクトルの大きさを変えない一次変換とはどのようなものでしょうか? それは……もちろん回転です。つまり Q に z と z の共役複素数を掛けたものは、Q のベクトル部を z のベクトル部を軸として回転させたものだったのです。
簡単な例で試してみましょう。ベクトル V = (1,0,0) と、対応するクォータニオン Q = 0 + i を考えます。z軸周りの回転を表すクォータニオン z は a + ck と書けるので、共役複素数は、
Q' = (a + ck)(i)(a + ck)-1
z の逆数とは何でしょう? これはクォータニオン z の大きさが 1 となるように a と c を選ぶことによって、逆数と共役複素数が同じであることが簡単に分かります。
len(z) = 1 = zz* ゆえに z* = z-1
よって、書き直すと
Q' = (a + ck)(i)(a - ck) = (a + ck)(ai + cj) = a2i + acj + caj - c2i = (a2- c2)i + 2acj
条件から
a2+ c2 = 1
ゆえに、ある角度θを用いて書くと a = cos(θ/2), b = sin(θ/2) (1/2を掛けた理由はもうすぐわかります。)
i と j の項はそれぞれ下記を満たします。
cos2(θ/2) - sin2(θ/2) = cos(θ)
かつ
2 cos(θ/2) sin(θ/2) = sin(θ)
これは確かに k (z) 軸周りにθだけ回転させた回転を表しています。一般化すると、ベクトル V を軸 A = (b,c,d) (正規化されていると仮定します。つまり ||A|| = 1 です。)周りに角度θだけ回転させるクォータニオンは
z = cos(θ/2) + sin(θ/2)A = cos(θ/2) + sin(θ/2){bi + cj + dk}
すると、 Q = 0 + V の共役複素数と z について、
Q' = zQz*
ベクトル部だけを抜き出すと
Q' = 0 + V'
V' の正体はベクトル V を回転させたものです。
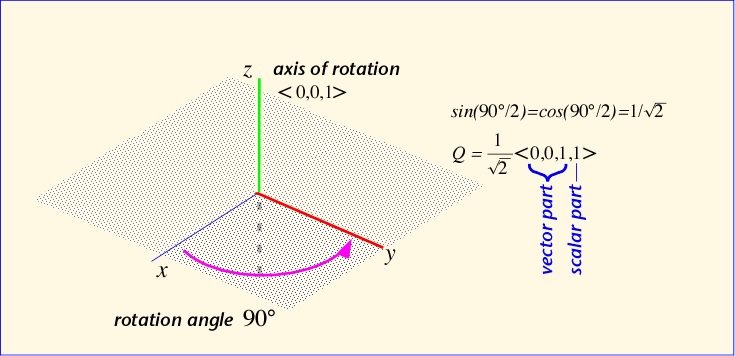
Second Life では、回転を表わすクォータニオンは浮動小数点数4つで表現されます。最初の3つがベクトル部で、最後の1つがスカラー部です。つまり Q = <Q.x, Q.y, Q.z, Q.s> となっています。 Second Lifeの地域における方角について、東西方向がx軸、南北方向がy軸、上下方向がz軸となっています。x は 虚軸の i 軸への、y は j への、z は k への写像でしたね。これは右手系座標であることがわかります。右手系座標とは右手と方向付けが同じで、手を開いて x 軸のプラスの方角(東の方角)へ向けたとき、曲げた指が y 軸のプラス(北の方角)を向き、親指を手のひらの成す平面と曲げた指に垂直に立てると z 軸のプラス(上方向)を向きます。回転角はラジアン単位で -π から π (パイ)までと決められています。つまり反時計回り(正の向き - x 軸のプラス側(東)から y 軸のプラス側(北)を通って x 軸のマイナス側(西)へ向かう向き)に半回転、または時計回り(負の向き - x 軸のプラス側(東)から y 軸のマイナス側(南)を通って x 軸のマイナス側(西)へ向かう向き)に半回転まで回転させることができ、回転角が3.141ラジアンもしくは180度のときには2つの向きによる回転は同じ結果になります。例えば西を向いている面を z 軸周りに反時計回りで90度回転させる(南を向く) rotation は、
<0, 0, 0.707, 0.707>
sinπ/4 と cosπ/4 (π/4 は回転角の半分) は両方とも 1/20.5 だからです。
同じく、回転させて東に向けるには、
<0, 0, 1, 0> と <0, 0, -1, 0> のどちらでもいいです。
オブジェクトを右に傾ける(x 軸の周りに反時計回りで回転させる)、例えば90度傾けるには、
<0.707, 0, 0, 0.707>
同じ角度、前に倒す(y 軸周りに時計回りで回転させる)には、
<0, -0.707, 0, 0.707>
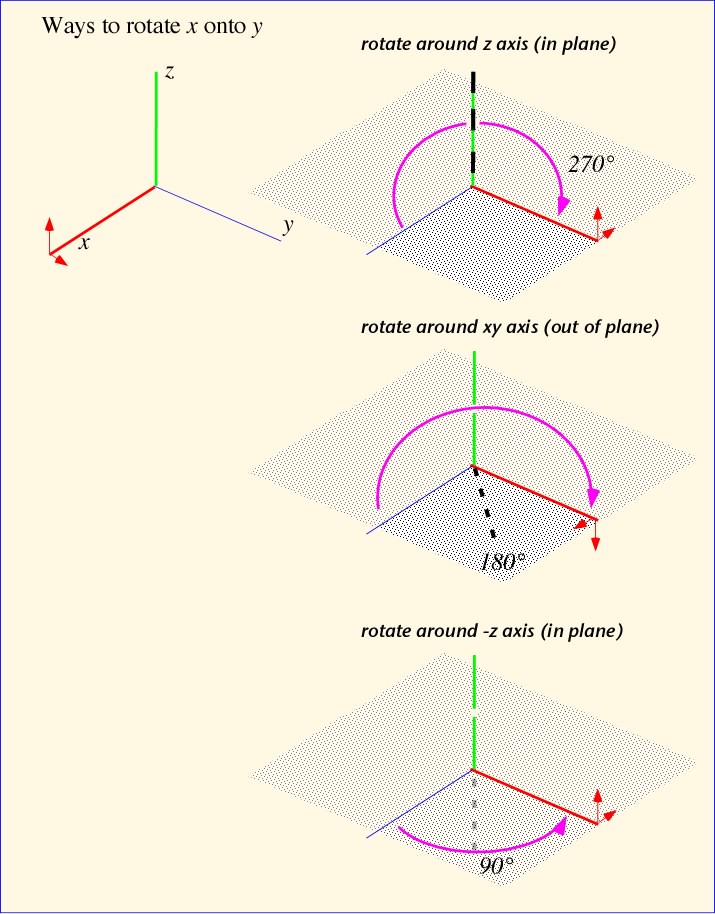
重要なのは、ベクトルの写像はクォータニオンによる回転と一対一対応しないということです。例えば下の図は x 軸から y 軸への何通りかの回転です。異なる回転は最終的な(y と z に)垂直な方向の向きが異なる結果になります。