Quaternion/fr

quaternion

Un mot-clé accepté par le compilateur, qui signifie la même chose que rotation et est interchangeable avec lui.

Définition et propriétés

Les quaternions sont une généralisation des nombres complexes inventée par William Rowan Hamilton au milieu du 19ème siècle. Rappelez-vous qu'un nombre complexe est la somme d'un nombre réel ordinaire a et d'un nombre imaginaire bi, où i est défini par :

i² = -1

Pour construire un quaternion, nous introduisons des unités imaginaires généralisées j et k avec les hypothèses :

j² = -1 ; k² = -1 ; ijk = -1

À partir de ces définitions de base il est facile de dériver les relations multiplicatives entre ces quantités imaginaires généralisées :

ij = k ; jk = i ; ki = j

et

ji = -k ; kj = -i ; ik = -j

Cela veut dire que la multiplication des quaternions n'est pas commutative. Bien que les opérations non commutatives soient de nos jours une caractéristique familière de l'algèbre linéaire, à l'époque de leur invention l'idée était révolutionnaire.

Un quaternion est donc un nombre de la forme

Q = a + bi + cj + dk

où a, b et c sont des nombres réels ordinaires. Ajouter des quaternions est assez facile, on ajoute simplement les facteurs correspondants :

a + bi + cj + dk + e + fi + gj + hk = ( a+e) + (b+f)i + (c+g)j + (d+h)k

Le résultat de la multiplication de deux quaternions peut être déduit des relations multiplicatives précédentes, en se souvenant de conserver l'ordre des termes en i, j et k puisque les unités imaginaires ne commutent pas.

QR = (a + bi + cj + dk)(e + fi + gj + hk) =

ae + afi + agj + ahk + bei - bf + bgij + bhik + cej + cfji - cg + chjk + dek + dfki + dgkj - dh

= ae + afi + agj + ahk + bei - bf + bgk - bhj + cej - cfk - cg + chi + dek + dfj - dgi - dh

= (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag -bh + ce + df)j + (ah + bg - cf + de)k

(... et vous qui pensiez que la multiplication des nombres complexes était compliquée !)

À présent, nous pouvons définir l'équivalent du conjugué d'un nombre complexe (nous utiliserons la notation *, mais d'autres notations sont également répandues) :

Q*= a - bi - cj - dk

Le produit d'un quaternion et de son conjugué est :

QQ* = (a + bi + cj + dk)(a - bi - cj - dk) =

= (a² + b² + c² + d²) + (-ab + ba - cd + dc)i + (-ac + bd + ca - db)j + (-ad - bc + cb + da)k

= (a² + b² + c² + d²)

ce qui ressemble drôlement au carré d'une longueur euclidienne. Si nous considérons le triplet (b, c, d) comme un vecteur V, nous pouvons réécrire cette longueur au carré comme :

QQ* = a² + ||V||²

Le premier terme, a, est souvent désigné comme le scalaire, ou parfois comme la partie réelle du quaternion, et le triplet (b, c, d) comme la partie vectorielle.

Quaternions et rotations

La raison qui nous fait nous intéresser aux quaternions est que Second Life les utilise pour représenter des rotations. Comment cela ? Considerons la représentation sous forme de quaternion d'un vecteur V = (b, c, d), c'est-à-dire simplement un quaternion avec une partie réelle nulle :

Q(V) = 0 + bi + cj + dk

Si nous multiplions Q par un autre quaternion, en général nous obtenons une partie réelle non nulle ; en d'autres termes, nous avons transformé le vecteur en un quaternion qui n'est pas un vecteur, ce qui ne ressemble pas du tout à l'effet attendu d'une rotation. Néanmoins, si nous multiplions d'un côté par un quaternion z, et de l'autre côté par l'inverse pour la multiplication de z, z^-1, nous obtenons un résultat avec une partie réelle nulle :

Re[zQ(V)z^-1] = 0

-- en fait, nous avons transformé un vecteur en vecteur. Pour s'assurer qu'il en est bien ainsi, on remarque que dans les formules de multiplication, la partie réelle de deux quaternions ne dépend pas de l'ordre de multiplication, c'est-à-dire :

Re[QR] = Re[RQ].

Nous pouvons donc inverser l'ordre du premier et du troisième quaternions dans la transformation sans changer la partie réelle :

Re[z(Q(V)z^-1)] = Re[(Q(V)z^-1)z] = Re[Q(V)(z^-1z)] = Re[Q(V)(1)] = 0

puisque la multiplication des quaternions est associative et que nous avions supposé que Q a une partie réelle nulle. Cette opération consistant à multiplier à gauche par un quaternion et à droite par son inverse est connue sous le nom de conjugaison par z. Les lecteurs familiers avec le calcul matriciel verront la ressemblance avec la décomposition d'une matrice en une rotation et un pur changement d'échelle (une matrice diagonale).

À quelle condition le conjugué d'un quaternion est-il identique au quaternion de départ ?

zQz^-1 = Q implique zQ = Qz

(ce que l'on peut démontrer facilement en multipliant la première expression à droite par z). Quand les quaternions commutent-ils ? Si l'on revient à l'expression du produit de deux quaternions, en se souvenant que les parties réelles commutent de toute façon, nous avons par exemple pour la partie facteur de i :

(af + be + ch - dg)i + ... = (eb+ fa + gd - hc)i + ...

lorsque la multiplication est commutative. Cela ne peut être vrai que si ch - dg = 0, soit c/d = g/h : dans le cas où la pente de la partie vectorielle dans le plan (j, k) est la même pour les deux quaternions. En reprenant le même raisonnement pour les parties facteur de j et de k, il doit également en être de même dans les plans (i, j) et (i, k) : les deux quaternions doivent avoir des vecteurs qui pointent dans la même direction. Q et R doivent avoir des parties vectorielles colinéaires.

Il n'est pas dur non plus de voir que la conjugaison est également linéaire (que le conjugué d'une somme est égal à la somme des conjugués), et il est facile de voir que la longueur de la partie vectorielle de Q est préservée par conjuguaison. Quelle sorte de transformation conservant la longueur ne préserve un vecteur que lorsque son axe coincide avec le vecteur ? Mais -- une rotation, bien sûr. Ainsi, conjuguer Q par z revient à tourner la partie vectorielle de Q autour de l'axe défini par la partie vectorielle de z.

Essayons sur un cas simple. Considérons le vecteur V = (1, 0, 0) et le quaternion correspondant Q = 0 + i. Pour tourner autour de l'axe des z, nous avons besoin d'un quaternion de la forme a + ck. Le conjugué est alors :

Q' = (a+ck) (i) (a + ck)^-1

Quel est l'inverse de z ? Il est facile de voir que si nous choisissons a et c de manière à ce que la longueur du quaternion soit 1, alors l'inverse est égal au conjugué :

longueur(z) = 1 = zz* implique z* = z^-1

ainsi nous pouvons écrire :

Q' = (a+ck) (i) (a - ck) = (a+ck) (ai + cj) = a²i + acj + caj - c²i = ( a²- c²)i + 2acj

La contrainte :

a²+ c² = 1

implique que nous pouvons écrire a = cos(θ/2), b = sin(θ/2) pour un certain angle θ (la raison d'être du facteur 1/2 sera expliquée dans un moment).

Les termes en i et j deviennent respectivement :

cos²(θ/2) - sin²(θ/2) = cos(θ)

et

2 cos(θ/2) sin(θ/2) = sin(θ)

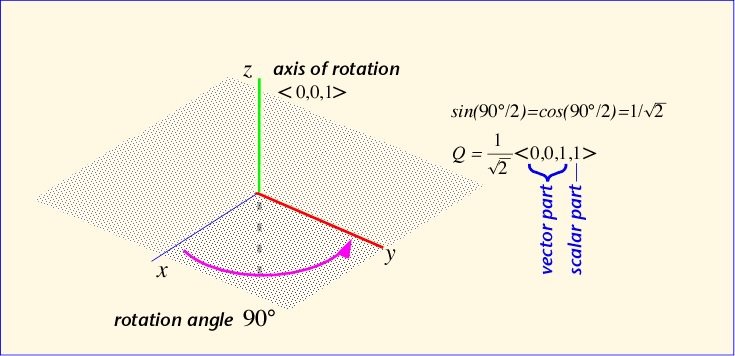
Cela représente bien une rotation de i d'un angle θ. Nous pouvons généraliser cela, pour tourner un vecteur V autour d'un axe porté par un vecteur unitaire A= (b, c, d) (||A|| = 1) d'un angle θ, nous construisons le quaternion

z = cos(θ/2) + sin(θ/2)A = cos(θ/2) + sin(θ/2){bi + cj + dk}

et nous conjuguons ensuite le quaternion Q = 0 + V par z :

Q' = zQz*

duquel nous extrayons la partie vectorielle :

Q' = 0 + V' => V' qui est le vecteur tourné V.

In Second Life, quaternions representing rotations are given as four real numbers. The first three are the vector part, and the last is the scalar part: Q = (Q.x, Q.y, Q.z, Q.s). In terms of Second Life region directions, the East-West direction is the x-axis, the North-South direction is the y-axis, and the Up-Down direction is the z-axis. Recall that x maps to the imaginary i axis, y to j, and to z to k. We can see that this is a right-handed coordinate system: if you wrap the fingers of your right hand from x to y, your thumb will point in the z direction. Default angles of rotation are defined in radians, from -π to π; that is, we can rotate counter-clockwise (in the positive direction) half-way around, or in the clockwise (negative) direction half-way around, with the two directions giving the same physical result at a rotation angle of 3.141 radians or 180 degrees. Thus a counter-clockwise rotation of a face pointing West, around the z axis by 90 degrees (to point South) is:

(0,0,0.707,0.707)

since the sine and cosine of π/4 (half of the rotation angle) are both 1/2^0.5.

Continuing around to point East is either

(0,0,1,0) or (0,0,-1,0)

Tilting an object to the right (that is, rotating it counter-clockwise around the x-axis) by e.g. 90 degrees is described by:

(0.707,0,0,0.707)

and pitching forward (clockwise around the y-axis) by the same amount is

(0,-0.707,0,0.707).

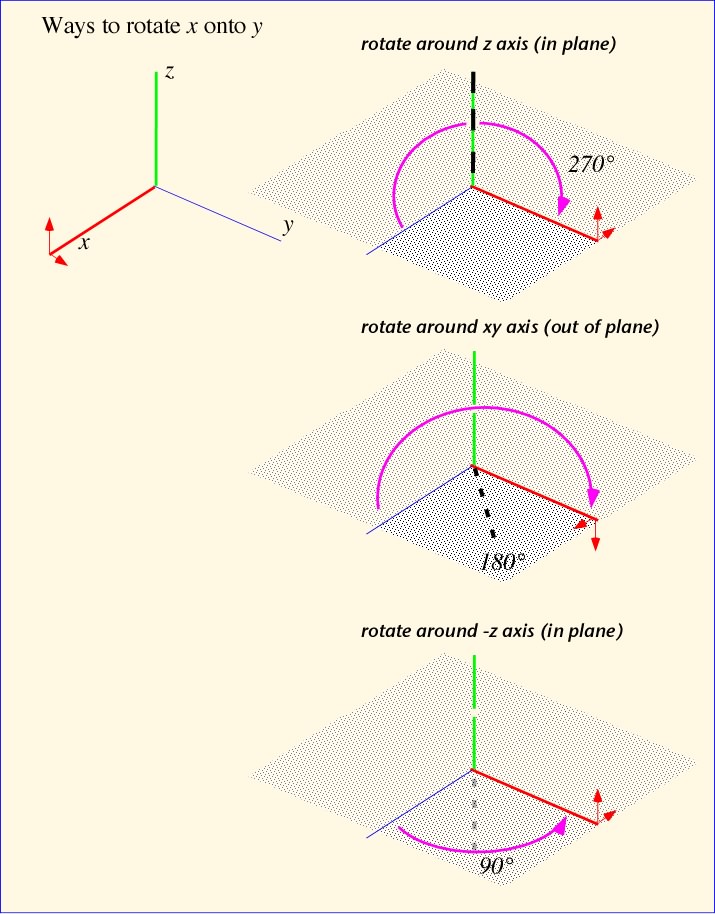
It's important to note that the mapping of a single vector does not uniquely specify the corresponding quaternion rotation. For example, in the figure below we see a number of ways to rotate the x axis into the y axis. Different rotations result in different final orientations of the orthogonal (y and z) directions.