Difference between revisions of "Quaternion/fr"
m (grrr) |
m (Translated one more paragraph) |
||
| Line 2: | Line 2: | ||
==quaternion== | ==quaternion== | ||
Un mot-clé accepté par le compilateur qui signifie la même chose que {{LSLG|rotation/fr|rotation}} et est interchangeable avec lui. | Un mot-clé accepté par le compilateur, qui signifie la même chose que {{LSLG|rotation/fr|rotation}} et est interchangeable avec lui. | ||
[[Category:LSL Types/fr|Quaternion/fr|Quaternion]] | [[Category:LSL Types/fr|Quaternion/fr|Quaternion]] | ||
| Line 8: | Line 8: | ||
== | == Définition et propriétés == | ||
Les quaternions sont une généralisation des nombres complexes inventée par William Rowan Hamilton au milieu du 19ème siècle. Rappelez-vous qu'un nombre complexe est la somme d'un nombre réel ordinaire a et d'un nombre imaginaire bi, où i est défini par : | |||
i<sup>2</sup> = -1 | i<sup>2</sup> = -1 | ||
Pour construire un quaternion, nous introduisons des unités imaginaires généralisées j et k avec les hypothèses : | |||
j<sup>2</sup> = -1; k<sup>2</sup> = -1; ijk = -1 | j<sup>2</sup> = -1 ; k<sup>2</sup> = -1 ; ijk = -1 | ||
À partir de ces définitions de base il est facile de dériver les relations multiplicatives entre ces quantités imaginaires généralisées : | |||
ij = k; jk = i; ki = j | ij = k ; jk = i ; ki = j | ||
et | |||
ji = -k; kj = -i; ik = -j | ji = -k ; kj = -i ; ik = -j | ||
Cela veut dire que la multiplication des quaternions n'est pas commutative. Bien que les opérations non commutatives soient de nos jours une caractéristique familière de l'algèbre linéaire, à l'époque de leur invention l'idée était révolutionnaire. | |||
Un quaternion est donc un nombre de la forme | |||
Q = a + bi + cj + dk | Q = a + bi + cj + dk | ||
où a, b et c sont des nombres réels ordinaires. Ajouter des quaternions est assez facile, on ajoute simplement les facteurs correspondants : | |||
a + bi + cj + dk + e + fi + gj + hk = ( a+e) + (b+f)i + (c+g)j + (d+h)k | a + bi + cj + dk + e + fi + gj + hk = ( a+e) + (b+f)i + (c+g)j + (d+h)k | ||
Le résultat de la multiplication de deux quaternions peut être déduit des relations multiplicatives précédentes, en se souvenant de conserver l'ordre des termes en i, j et k puisque les unités imaginaires ne commutent pas. | |||
QR = (a + bi + cj + dk)(e + fi + gj + hk) = | QR = (a + bi + cj + dk)(e + fi + gj + hk) = | ||
| Line 53: | Line 53: | ||
= (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag -bh + ce + df)j + (ah + bg - cf + de)k | = (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag -bh + ce + df)j + (ah + bg - cf + de)k | ||
( | (... et vous qui pensiez que la multiplication des nombres complexes était compliqué !) | ||
À présent, nous pouvons définir l'équivalent du conjugué d'un nombre complexe (nous utiliserons la notation *, mais d'autres notations sont également répandues) : | |||
Q*= a - bi - cj - dk | Q*= a - bi - cj - dk | ||
Le produit d'un quaternion et de son conjugué est : | |||
QQ* = (a + bi + cj + dk)(a - bi - cj - dk) = | QQ* = (a + bi + cj + dk)(a - bi - cj - dk) = | ||
| Line 67: | Line 67: | ||
= (a<sup>2</sup> + b<sup>2</sup> + c<sup>2</sup> + d<sup>2</sup>) | = (a<sup>2</sup> + b<sup>2</sup> + c<sup>2</sup> + d<sup>2</sup>) | ||
ce qui ressemble drôlement au carré d'une longueur euclidienne. Si nous considérons le triplet (b, c, d) comme un vecteur V, nous pouvons réécrire cette longueur au carré comme : | |||
QQ* = a<sup>2</sup> + ||V||<sup>2</sup> | QQ* = a<sup>2</sup> + ||V||<sup>2</sup> | ||
Le premier terme, a, est souvent désigné comme le scalaire, ou parfois comme la partie réelle du quaternion, et le triplet (b, c, d) comme la partie vectorielle. | |||
== Quaternions | == Quaternions et rotations == | ||
The reason we care about quaternions is that Second Life uses them to represent rotations. How is this done? Consider the quaternion representation of a vector V = (b,c,d), which is just a quaternion with a zero real part: | The reason we care about quaternions is that Second Life uses them to represent rotations. How is this done? Consider the quaternion representation of a vector V = (b,c,d), which is just a quaternion with a zero real part: | ||
Revision as of 13:33, 5 December 2007
| LSL Portal | Functions | Events | Types | Operators | Constants | Flow Control | Script Library | Categorized Library | Tutorials |
quaternion
Un mot-clé accepté par le compilateur, qui signifie la même chose que rotation et est interchangeable avec lui.
Définition et propriétés
Les quaternions sont une généralisation des nombres complexes inventée par William Rowan Hamilton au milieu du 19ème siècle. Rappelez-vous qu'un nombre complexe est la somme d'un nombre réel ordinaire a et d'un nombre imaginaire bi, où i est défini par :
i2 = -1
Pour construire un quaternion, nous introduisons des unités imaginaires généralisées j et k avec les hypothèses :
j2 = -1 ; k2 = -1 ; ijk = -1
À partir de ces définitions de base il est facile de dériver les relations multiplicatives entre ces quantités imaginaires généralisées :
ij = k ; jk = i ; ki = j
et
ji = -k ; kj = -i ; ik = -j
Cela veut dire que la multiplication des quaternions n'est pas commutative. Bien que les opérations non commutatives soient de nos jours une caractéristique familière de l'algèbre linéaire, à l'époque de leur invention l'idée était révolutionnaire.
Un quaternion est donc un nombre de la forme
Q = a + bi + cj + dk
où a, b et c sont des nombres réels ordinaires. Ajouter des quaternions est assez facile, on ajoute simplement les facteurs correspondants :
a + bi + cj + dk + e + fi + gj + hk = ( a+e) + (b+f)i + (c+g)j + (d+h)k
Le résultat de la multiplication de deux quaternions peut être déduit des relations multiplicatives précédentes, en se souvenant de conserver l'ordre des termes en i, j et k puisque les unités imaginaires ne commutent pas.
QR = (a + bi + cj + dk)(e + fi + gj + hk) =
ae + afi + agj + ahk + bei - bf + bgij + bhik + cej + cfji - cg + chjk + dek + dfki + dgkj - dh
= ae + afi + agj + ahk + bei - bf + bgk - bhj + cej - cfk - cg + chi + dek + dfj - dgi - dh
= (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag -bh + ce + df)j + (ah + bg - cf + de)k
(... et vous qui pensiez que la multiplication des nombres complexes était compliqué !)
À présent, nous pouvons définir l'équivalent du conjugué d'un nombre complexe (nous utiliserons la notation *, mais d'autres notations sont également répandues) :
Q*= a - bi - cj - dk
Le produit d'un quaternion et de son conjugué est :
QQ* = (a + bi + cj + dk)(a - bi - cj - dk) =
= (a2 + b2 + c2 + d2) + (-ab + ba - cd + dc)i + (-ac + bd + ca - db)j + (-ad - bc + cb + da)k
= (a2 + b2 + c2 + d2)
ce qui ressemble drôlement au carré d'une longueur euclidienne. Si nous considérons le triplet (b, c, d) comme un vecteur V, nous pouvons réécrire cette longueur au carré comme :
QQ* = a2 + ||V||2
Le premier terme, a, est souvent désigné comme le scalaire, ou parfois comme la partie réelle du quaternion, et le triplet (b, c, d) comme la partie vectorielle.
Quaternions et rotations
The reason we care about quaternions is that Second Life uses them to represent rotations. How is this done? Consider the quaternion representation of a vector V = (b,c,d), which is just a quaternion with a zero real part:
Q(V) = 0 + bi + cj + dk
If we multiply Q by some other quaternion, in general we will get a non-zero real part; that is, we've transformed the vector into a non-vector quaternion, which doesn't look at all like a rotation. However, if we multiply on one side by a quaternion z, and on the other side by the multiplicative inverse of z, z-1, we will get a result with a 0-value real part:
Re[zQ(V)z-1] = 0
-- that is, we'll map a vector into a vector. To see that this is so, note that from the formula for multiplication, the real part of the product of two quaternions is invariant to the order of multiplication, that is:
Re[QR] = Re[RQ].
So we can invert the order of the first and (second*third) quaternions in the mapping without changing the real part:
Re[z(Q(V)z-1)] = Re[(Q(V)z-1)z] = Re[Q(V)(z-1z)] = Re[Q(V)(1)] = 0
since quaternion multiplication is associative and we assumed that Q has a zero-value real part. This operation of left-multiplying by a quaternion and right-multiplying by its inverse is known as conjugation by z. Readers familiar with matrix algebra will recognize it as similar to the decomposition of a matrix into a rotation and a pure scaling (a diagonal matrix).
Under what conditions does conjugation of a quaternion give back the original quaternion?
zQz-1 = Q implies zQ = Qz
(which can be easily shown by right-multiplying the first expression by z). When do quaternions commute? From the expression for the product of two quaternions, recalling that the real parts commute in general, we have for example for the part multiplying i:
(af + be + ch - dg)i + ... = (eb+ fa + gd - hc)i + ...
in the case where multiplication is commutative. This can only be true if ch - dg = 0 or c/d = g/h: that is, the slope of the vector part in the (j,k) plane is the same for both quaternions. Since there's nothing special about i, this must also be true of the (i,j) and (i,k) planes: that is, the two quaternions must have vectors that point in the same direction. Q and R must have vector parts that are collinear. It's not too hard to show that conjugation is also linear (that is, the conjugate of the sum is the sum of the conjugates), and it's easy to see that the length of the vector part of Q is preserved under conjugation. What sort of length-conserving linear transformation preserves a vector only when its axis coincides with the vector? Why -- a rotation, of course. So conjugation of Q by z is equivalent to rotating the vector part of Q around the axis defined by the vector part of z.
Let's try a simple case. Consider the vector V = (1,0,0) and corresponding quaternion Q = 0 + i. To rotate around the z-axis we need a quaternion z of the form a + ck. The conjugation is then:
Q' = (a+c k)(i)(a + ck)-1
What is the inverse of z? It's easy to see that if we choose a and c so that the length of the quaternion is 1, then the inverse is equal to the conjugate:
len(z) = 1 = zz* implies z* = z-1
so we can write:
Q' = (a+c k)(i)(a - ck) = (a+c k)(ai + cj) = a2i + acj + caj - c2i = ( a2- c2)i + 2acj
with the constraint:
a2+ c2 = 1
implying that we can write a = cos(θ/2), b = sin(θ/2) for some angle θ (the reason for the factor of 1/2 will become clear in a moment).
Now, the terms in i and j become respectively:
cos2(θ/2) - sin2(θ/2) = cos(θ)
and
2 cos(θ/2) sin(θ/2) = sin(θ)
So this indeed represents a rotation of the i (x) axis by the angle θ. We can infer that in the general case, to rotate a vector V around an axis A= (b,c,d) (presumed normalized, that is ||A|| = 1) by an angle θ, we construct the quaternion
z = cos(θ/2) + sin(θ/2)A = cos(θ/2) + sin(θ/2){bi + cj + dk}
and then conjugate the quaternion Q = 0 + V with z :
Q' = zQz*
from which we extract the vector part:
Q' = 0 + V' => V' being the rotated vector V.
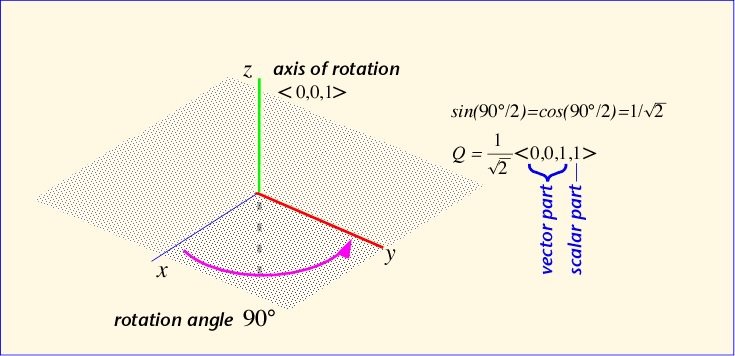
In Second Life, quaternions representing rotations are given as four real numbers. The first three are the vector part, and the last is the scalar part: Q = (Q.x, Q.y, Q.z, Q.s). In terms of Second Life region directions, the East-West direction is the x-axis, the North-South direction is the y-axis, and the Up-Down direction is the z-axis. Recall that x maps to the imaginary i axis, y to j, and to z to k. We can see that this is a right-handed coordinate system: if you wrap the fingers of your right hand from x to y, your thumb will point in the z direction. Default angles of rotation are defined in radians, from -π to π; that is, we can rotate counter-clockwise (in the positive direction) half-way around, or in the clockwise (negative) direction half-way around, with the two directions giving the same physical result at a rotation angle of 3.141 radians or 180 degrees. Thus a counter-clockwise rotation of a face pointing West, around the z axis by 90 degrees (to point South) is:
(0,0,0.707,0.707)
since the sine and cosine of π/4 (half of the rotation angle) are both 1/20.5.
Continuing around to point East is either
(0,0,1,0) or (0,0,-1,0)
Tilting an object to the right (that is, rotating it counter-clockwise around the x-axis) by e.g. 90 degrees is described by:
(0.707,0,0,0.707)
and pitching forward (clockwise around the y-axis) by the same amount is
(0,-0.707,0,0.707).
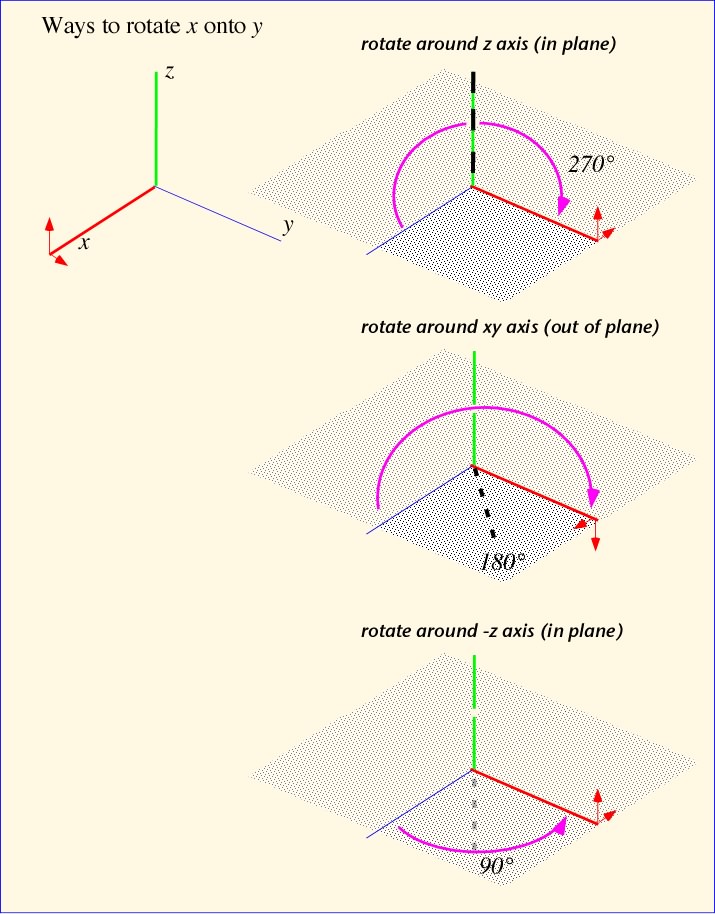
It's important to note that the mapping of a single vector does not uniquely specify the corresponding quaternion rotation. For example, in the figure below we see a number of ways to rotate the x axis into the y axis. Different rotations result in different final orientations of the orthogonal (y and z) directions.