Difference between revisions of "Interpolation/Linear"
Jump to navigation
Jump to search
(Created page with "{{LSL Header|Interpolation}} {{RightToc|clear:right;}} == Linear Interpolation == {|cellspacing="0" cellpadding="3" border="1" style="border: 1px solid #aaaaaa; margin: 1em…") |
|||
| Line 119: | Line 119: | ||
| return rotation rLin | | return rotation rLin | ||
| Returns spherical linear interpolation of two rotations | | Returns spherical linear interpolation of two rotations | ||
|} | |||
| Graph goes here, k. | |||
|} | |||
<div style="float:right;font-size: 80%;"> | |||
Released to Public Domain. By Nexii Malthus</div> | |||
|} | |||
{|cellspacing="0" cellpadding="3" border="1" style="border: 1px solid #aaaaaa; margin: 1em 1em 1em 0pt; background-color: #ffffff; border-collapse: collapse" width="80%" | |||
!style="color: #000000; background-color: #aaaaff;" height="20px"| | |||
===Vector List, Linear=== | |||
|- | |||
| | |||
Interpolates between two vectors in a list of vectors. | |||
<lsl> | |||
vector pLin(list v, float t, integer Loop ){ | |||
float l = llGetListLength(v); t *= l-1; | |||
float f = (float)llFloor(t); | |||
integer i1 = 0; integer i2 = 0; | |||
if(Loop){ i1 = (integer)(f-llFloor(f/l)*l); | |||
++f;i2 = (integer)(f-llFloor(f/l)*l);} | |||
else { | |||
if( f > l-1 ) i1 = (integer)l-1; | |||
else if( f >= 0 ) i1 = (integer)f; | |||
if(f+1 > l-1 ) i2 = (integer)l-1; | |||
else if(f+1 >= 0 ) i2 = (integer)f+1; } | |||
vector v1 = llList2Vector(v, i1); | |||
vector v2 = llList2Vector(v, i2); | |||
return vLin( v1, v2, t-f );} | |||
</lsl> | |||
{|cellspacing="0" cellpadding="3" border="1" style="border: 1px solid #aaaaaa; margin: 1em 1em 1em 0pt; background-color: #ffffff; border-collapse: collapse" width="80%" | |||
| | |||
{|cellspacing="0" cellpadding="6" border="1" style="border: 1px solid #aaaaaa; margin: 1em 1em 1em 0pt; background-color: #e0e0ff; border-collapse: collapse" | |||
!style="background-color: #d0d0ee" | Input | |||
!style="background-color: #d0d0ee" | Description | |||
|- | |||
| list v | |||
| A path of vectors. | |||
|- | |||
| float t | |||
| Interpolation, Start 0.0 - 1.0 End. | |||
|- | |||
| integer Loop | |||
| Whether the list loops over. | |||
|- | |||
!style="background-color: #d0d0ee" | Output | |||
!style="background-color: #d0d0ee" | Description | |||
|- | |||
| return vector pLin | |||
| Returns a vector that is the linear interpolation of two vectors between 't'. | |||
|} | |} | ||
| Graph goes here, k. | | Graph goes here, k. | ||
Revision as of 12:40, 4 September 2011
| LSL Portal | Functions | Events | Types | Operators | Constants | Flow Control | Script Library | Categorized Library | Tutorials | Interpolation |
Linear Interpolation
Float Linear | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
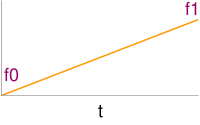
Linear interpolation of f0 and f1 with fraction t. <lsl> float fLin(float f0,float f1,float t) { return f0*(1-t) + f1*t; } </lsl>
Released to Public Domain. By Nexii Malthus
|
Vector Linear | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Linear interpolation of v0 and v1 with fraction t. <lsl> vector vLin(vector v0, vector v1,float t){ return v0*(1-t) + v1*t; } </lsl>
Released to Public Domain. By Nexii Malthus
|
Rotation Linear | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Spherical Linear interpolation of r0 and r1 with fraction t. Also known as SLERP <lsl> rotation rLin(rotation r0,rotation r1,float t) { float ang = llAngleBetween(r0, r1); if(ang > PI) ang -= TWO_PI; return r0 * llAxisAngle2Rot( llRot2Axis(r1/r0)*r0, ang*t); } </lsl>
Released to Public Domain. By Nexii Malthus
|
Vector List, Linear | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Interpolates between two vectors in a list of vectors. <lsl> vector pLin(list v, float t, integer Loop ){ float l = llGetListLength(v); t *= l-1;
float f = (float)llFloor(t);
integer i1 = 0; integer i2 = 0;
if(Loop){ i1 = (integer)(f-llFloor(f/l)*l);
++f;i2 = (integer)(f-llFloor(f/l)*l);}
else {
if( f > l-1 ) i1 = (integer)l-1;
else if( f >= 0 ) i1 = (integer)f;
if(f+1 > l-1 ) i2 = (integer)l-1;
else if(f+1 >= 0 ) i2 = (integer)f+1; }
vector v1 = llList2Vector(v, i1);
vector v2 = llList2Vector(v, i2);
return vLin( v1, v2, t-f );}
</lsl>
Released to Public Domain. By Nexii Malthus
|