Linkability Rules/it

/it

Quando le prim sono linkabili

Considerate due primitive, A e B. Per determinare se queste possono essere collegate o meno si calcola lo spazio dal bordo della sfera che racchiude l'oggetto al bordo opposto dall'altra sfera e confrontandolo con il valore di massima distanza di linkabilità, che è una funzione dei raggi delle due sfere:

    (1) massima_distanza_link = minimo( 3 * (raggio_di_A + raggio_di_B) + distanza_minima, distanza_massima)

Dove:

    (2) distanza_minima = 1,0 metri 
    (3) distanza_massima = 54,0 metri
    (4) raggio_X = raggio della sfera contenente la primitiva X (Figura A)
    (5) minimo (C, D) = al minimo tra C e D

Se la distanza misurata tra le due sfere è inferiore o uguale al massima_distanza_link allora le corrispondenti primitive possono essere linkate tra loro. In termini matematici:

    (6) A_può_linkare_B = lunghezza (centro_di_A - centro_di_B) + raggio_di_A + raggio_di_B <= massima_distanza_link)

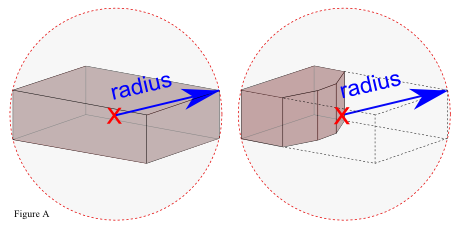
La bounding sphere è la più piccola sfera che racchiude tutto il bounding box locale di una primitiva.

Il local bounding box è il cubo centrato nella primitiva nel suo centro geometrico con il sistema di riferimento locale e di dimensioni uguali alla dimensione della primitiva.

Il centro geometrico della primitiva è il suo centro di simmetria locale calcolato prima delle operazioni di cut, shear, twist, taper, e di hollow.

Nota che una bounding sphere di una primitiva non è necessariamente la sfera più stretta possibile per la sua forma, a meno che la primitiva non sia una semplice box. La sfera di bounding dipende esclusivamente dalla posizione della primitiva e dalle sue dimensioni, per cui qualsiasi cut o hollow della primitiva la renderà notevolmente più piccola della sua bounding sphere, e non necessariamente vicina al suo centro. Inoltre, una primitiva twistata o shearata può avere gli spigoli che si estendono al di fuori della sua sfera di bounding. Poiché le regole di Linkability dipendono solo dalla bounding sphere, che è in ultima analisi dipende solo dalla posizione della primitiva e dalle sue dimensioni, la linkabilità di due prims è indipendente dai cambiamenti della forma e di rotazione.

TODO - abbiamo bisogno di un nuovo figura_A che mostri Area, invecedi diametro. Anche bisogno di nuove figure e _B _C per due correlabili prims e due correlabili multi-cfr oggetti.

Algoritmo per la linkabilità

Le norme che disciplinano il linkability di oggetti multi-prim è molto simile al caso di due sole primitive. Si applica la stessa formula (1) e (6), ma la bounding sphere di un oggetto multi-prim sono le più piccole sfere che contengono completamente tutte le sfere di bounding delle corrispondenti primitive che si vogliono linkare.

Quando si collegano tre o più oggetti l'algoritmo itera tra gli oggetti candidati fino a quando tutte le prim linkabili sono state trovate. La prim principale dell'oggetto viene testata con ogni candidato e la sfera di bounding diventa più grande ad ogni collegamento calcolato andato a buon fine. Quindi qualsiasi prim scollegata viene testata e fusa man mano ottenendo collezioni più grandi secondo le formule. L'oggetto principale è quindi ri-testato contro la modifica e il processo continua fino a quando tutti gli oggetti sono collegati, o non vengono trovati nuovi collegamenti validi.

Casi di fallimento

Se un insieme non linkabile è testato dall'algoritmo di linkabilità il sottoinsieme finale delle parti linkabili è determinato dall'ordine in cui i candidati sono stati elaborati. La banale prova di questo si ha considerano primitiva root tra una griglia di tantissime altre primitive. L'algoritmo non riesce a linkare tutte queste primitive, ma se sono state testate prima tutte quelle a ovest alla fine il sottoinsieme delle prim linkate durante l'operazione di link potrebbe non poter collegare parte delle primitive a est che non superano il vincolo della distanza_massima (3). Il risultato finale potrebbe essere diverso se le primitive a est vengono testate prima delle altre.

Se un insieme linkabile è testato dall'algoritmo di linkabilità il sottoinsieme finale delle parti linkabili non è determinato dall'ordine in cui i candidati sono stati sottoposti. Ciò significa che, se i sottoinsiemi linkabili del caso precedente vengono testati per la linkabilità qualunque permutaziona dei suoi elementi sarà sempre linkabile a prescindere dall'ordine in cui vengono linkati. La prova di ciò è lasciata come un esercizio per il lettore.

Esempi

Due prim molto piccole

raggio_di_A = ~ 0,01

raggio_di_B = ~ 0,01

distanza_minima = 1,0 metri

distanza_massima = 54,0 metri

massima_distanza_link = 1.06m

Uno prim grande con un piccolo prim

raggio_di_A = 5m

raggio_di_B = ~ 0,01

distanza_minima = 1,0 metri

distanza_massima = 54,0 metri

3 * (raggio_di_A + raggio_di_B) + distanza_massima = 15,03 metri

15.03m è inferiore a 54.0m

Così la massima_distanza_link = 15.03m

Due prim molto grandi

Il diametro di una sfera bounding è la radice quadrata di x ^ 2 + y ^ 2 + z ^ 2

Quindi, il diametro della sfera che contiene il cubo di dimensioni 10m x 10m x 10m è la radice quadrata di (100 + 100 + 100) = ~ 17.3m

E il diametro di un 10m x 1m x 1m è radice quadrata (100 + 1 + 1) = ~ 10.1m

(Il tipo di prim non importa per questo calcolo. Sono importanti soltanto le dimensioni.)

Prendiamo il caso di due prim di dimensione 10m x 10m x 10m.

raggio_di_A = 8.66m

raggio_di_B = 8.66m

distanza_minima = 1,0 metri

distanza_massima = 54,0 metri

3 * (raggio_di_A + raggio_di_B) + distanza_minima = 52.96m

52.96m è inferiore a 54m

Così la massima_distanza_link = 52.96m