Linkability Rules/fr
Déterminer si un ensemble de prims ou d’objets peut être lié est une chose difficile à savoir.
En règle générale, les prims de grandes tailles peuvent être liées à de plus grandes distances, la distance max de liaison varie entre 2 et 54m. La distance max dépend de la position et de la taille de chaque prim, mais est indépendante de leur forme, de leur rotation ou d’un changement de taille (trou, découpage, etc).
En résumé
- Si la distance entre deux prims est trop importante, elles ne peuvent pas être liées.
- La distance autorisée est proportionnelle à la taille des objets à lier (des objets de grandes tailles pourront être liés à de plus grandes distances que des objets de petites tailles).
- Le calcul réel de la distance max tolérée est compliqué.
Présentation rapide

Présentation rapide de Kelly :
- Deux sphères peuvent être liées si leur boite de délimitation est entièrement incluse dans la "Sphère de liaison".
- La taille de la "sphère de liaison" varie de 2m à 54m en fonction de la taille des deux pièces à lier.
- La taille correspond à 3 fois la somme des rayons des sphères de délimitation plus deux et est plafonnée à 54m.
- Si vous liez plus de deux éléments, traitez les pièces liables deux par deux en appliquant la règle décrite ci dessus puis considérez les nouveaux éléments comme des pièces uniques dont la taille est déterminée à partir des pièces liées.
- Répéter cette opération jusqu’à ce que tous les éléments soient liés.
Dans le cas des nano-prims, deux pièces peuvent être liées si elles sont à moins de 2m l’une de l’autre. A l’opposé, les grandes prims doivent être incluses dans une sphère de 54m de diamètre.

- La possibilité de lier deux prims dépend uniquement de ses dimensions XYZ et de sa position, les autres propriétés (rotation, trou, découpages, sculpt, etc) sont ignorées. Cela signifie que les calculs sont réalisés en considérant chaque prim comme un cube ayant les dimensions X, Y, Z de l’objet à lier.
- Editer et sélectionner l’outil d’étirement d’une prim fera apparaître sa "boîte de délimitation"
- Les mégaprims : toute taille supérieure à 10 mètres est assimilée à une taille de 10m.
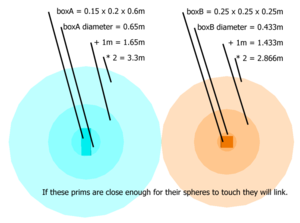
Une astuce pour imaginer le processus :
- Imaginez que toutes les prims soient transformées en leur boite de délimitation.
- Pour tous les éléments, imaginer à présent la plus petite sphère contenant chacune de ces boites.
- Ajoutez un mètre supplémentaire à chaque diamètre de sphère, puis doublez les. (Sans déplacer le centre des sphères). Vous obtenez ainsi de nouvelles sphères propres à chaque élément.
- Vous pouvez lier les objets si leur sphère se touchent ou se croisent. Liez tout ce qui peut l’être à ce stade.
- Exception : tout objet nécessitant une sphère supérieure à 54m est impossible à créer
- Répétez cette procédure avec les nouveaux éléments liés jusqu’à ce qu’il n’y ai plus aucun lien possible.

Lisez la section suivante pour obtenir des informations sur la formule de liaison (avec exemples et cas d’échec de liaison.)
Présentation détaillée
Prenez deux prims : A & B. Ces deux prims peuvent être liées si la distance séparant les bords opposées (les points les plus éloignés) des deux sphères de délimitation est inférieure à la distance max de liaison (fonction du rayon des deux sphères de délimitation)
(1) distance_max_liaison= minimum( 3 * (rayon_A + rayon_B) + BONUS_LIEN, DISTANCE_MAX )
Ou :
(3) BONUS_LIEN = 2.0 mètres (4) DISTANCE_MAX = 54.0 mètres (5) rayon_X = rayon de la sphère contenant la prim X (Figure A) (6) minimum(C, D) = renvoie la plus petite valeur entre C & D.
Si la distance entre les extrémités opposées des deux sphères de délimitation est inférieure ou égale à distance_max_liaison, alors les deux prims peuvent être liées. Pour résumer en termes mathématiques :
(7) A_lié_à_B = (distance(centre_A - centre_B) + rayon_A + rayon_B <= distance_max_liaison)
La sphère de délimitation est à la plus petite sphère capable d’entièrement inclure la boite de délimitation de l’objet.
La boite de délimitation est la boîte ayant le même centre géométrique et les mêmes dimensions XYZ que la prim. Pour les mégaprims les dimensions supérieures à 10m sont ramenées à 10m.
Le centre géométrique d’une prim est son centre de symétrie avant déformation (découpage, trouage, torsion, etc.)
A noter que la sphère de délimitation n’est pas nécessairement la plus petite sphère capable de contenir l’objet (sauf dans le cas d’un cube standard). La sphère de délimitation dépend uniquement de la position et de la taille de la prim, donc une prim coupée et trouée bien que plus petite aura la même sphère de délimitation et le même centre géométrique que la prim non coupée/trouée (la sphère n’est plus centré sur la prim coupée/trouée).
De même une prim trouée et/ou cisaillée peut voir certains de ses coins dépasser de la sphère de délimitation. Puisque les règles de liaison dépendent uniquement de la sphère de délimitation, qui elle même ne dépend que de la position et de la taille de la prim, la liaison de deux prims est indépendante des changements de formes et de rotations des prims.
TODO – A faire : une image figures _B and _C pour deux prim liables et deux objets multi prims liables
Algorithme de liaison

Les lois pilotant la liaison d’objets multi-prims sont très similaires à celles des objets à deux prims. Les mêmes formules (1) et (7) s’appliquent, à la différence que les sphères de délimitations d’objets multi-prims sont les plus petites sphères capables de contenir entièrement les sphères de délimitation des prims sélectionnées.
Lorsque vous liez 3 objets ou plus l’algorithme réalise une itération entre les éléments sélectionnés jusqu’à ce que tous les éléments liables aient été trouvés. La prim racine est testée avec toutes les prims, puis le calcul est relancé avec une sphère de délimitation incluant les éléments pouvant être liés à la prim racine. Les éléments non liés sont alors re-testés entre eux et liés selon la même formule. L’objet racine est alors re-testé avec les éléments éligibles et le processus continue jusqu’à ce que tous les objets soient liés ou qu’aucun nouveau lien ne soit possible.
Echec
Si un ensemble non liable est testé par l’algorithme, alors le résultat final sera déterminé par l’ordre dans lequel les éléments auront été sélectionnés. Un exemple simple consiste à imaginer une prim racine au milieu d’une grille infinie composée de prims. Toutes les prims ne peuvent être liées entre elles. Si l’algorithme commençait par les prims de l’ouest, il ne pourrait lier les prims de l’est à cause de la contrainte DISTANCE_MAX (4). Si l’algorithme commençait par l’est, le résultat serait différent.
Si un ensemble liable est testé par l’algorithme alors le résultat final est indépendant de l’ordre de sélection des prims. En conséquence, toutes les permutations possibles dans la sélection des prims aboutiront systématiquement à une liaison réussie. La démonstration de cette règle est laissée comme exercice au lecteur.
Formules
Rayon de la sphère de délimitation : SQRT(x^2 + y^2 + z^2)/2
Distance max de liaison (2 prims) : Minimum de (3 * (rayon_A + rayon_B) + BONUS_LIEN) et de 54
Distance entre les centres (2 prims) : Minimum de ((3 * (rayon_A + rayon_B) + BONUS_LIEN) - (rayon_A + rayon_B)) et 54 - (rayon_A + rayon_B).
Si la distance max de 54 n’est pas atteinte, la distance entre les centres peut être réduite à : RACINE_CARRE(Xa^2 + Ya^2 + Za^2) + RACINE_CARRE(Xb^2 + Yb^2 + Zb^2) + BONUS_LIEN
Exemples
Deux très petites prims
rayon_A = ~0.01 rayon_B = ~0.01
BONUS_LIEN= 2.0 mètres DISTANCE_MAX = 54.0 mètres
3 * (rayon_A + rayon_B) + BONUS_LIEN= 2.06 mètres
2.06 est inférieur à 54
Donc distance_max_liaison = 2.06m
Une grande et une petite prim
rayon_A = 8.66m (rayon pour une prim de 10x10x10m) rayon_B = ~0.01
BONUS_LIEN= 2.0 mètres DISTANCE_MAX = 54.0 mètres
3 * (rayon_A + rayon_B) + BONUS_LIEN= 28.01 mètres
28.01 est plus petit que 54.0
donc distance_max_liaison = 28.01m
A noter qu’il ne s’agit pas de la distance max entre les deux centres, mais la distance max entre les deux extrémités les plus éloignées des sphères de délimitation A et B.
Deux très grandes prims
Le diamètre d’une sphère de délimitation est la racine carrée de x^2 + y^2 + z^2 donc le diamètre pour une prim de 10m x 10m x 10m est la racine carrée de (100+100+100) = ~17.3m Et le diamètre pour une prim de 10m x 1m x 1m est la racine carrée de (100+1+1) = ~10.1m (Le type de prims n’influence pas le calcul. Seules les dimensions sont importantes.)
Prenons le cas de deux prims de 10m x 10m x 10m.
rayon_A = 8.66m rayon_B = 8.66m
BONUS_LIEN= 2.0 mètres DISTANCE_MAX = 54.0 mètres
3 * (rayon_A + rayon_B) + BONUS_LIEN= 53.96m
53.96 est plus petit que 54
donc distance_max_liaison = 53.96m
Notez bien que ce n’est pas la distance max entre les deux centres. Le centre de chaque prims est en fait à 8.66m à l’intérieur de la sphère de délimitation et donc la distance max entre les centres est en fait d’environ 36.64m.
Distance entre les centres : RACINE_CARRE(Xa^2 + Ya^2 + Za^2) + RACINE_CARRE(Xb^2 + Yb^2 + Zb^2) + BONUS_LIEN RACINE_CARRE(10^2+10^2+10^2) + RACINE_CARRE(10^2+10^2+10^2) + 2 RACINE_CARRE(300) + RACINE_CARRE(300) + 2
17.32 + 17.32 + 2 = 36.64m On retrouve bien les 36.64m.
Bugs
Des objets liables avec Havok1 ne le sont plus en Havok4
Les règles de liaison d’Havok4 sont généralement plus larges que celles d’Havok1, cependant quelques cas d’objets liables en Havok1 non liables en Havok4 existent.
Havok1 utilisait un algorithme dit d’"alignement axial des boîtes de délimitation" (AABB). Il en résultait que la distance maximale de laison de Havok1 (distance d’un coin de la boîte AABB à son coin opposé) est plus grande que le diamètre de la plus grande sphère de délimitation possible d’Havok4.
La max AABB était en réalité une boite d’environ 32 mètres de coté ==> la distance max était de 55.4 mètres. Cette boite d’Havok1 rentre donc presque entièrement dans la sphère de 54m de diamètre utilisée par Havok4... mais certains coins dépassent légèrement ==> Une maison entrant très exactement dans AABB peut par conséquent ne plus être liable dans Havok4.
Notez que "AA" signifie "Alignement Axial" et suppose qu’en cas de rotation de votre maison, la boite AABB restait alignée sur les axes du monde (Est, Nord et Haut) au risque de faire dépasser votre maison de la boite AABB. Dans ce genre de situation, l’objet est délié au premier redémarrage de la région ou lors de son rez (si vous l’aviez pris dans votre inventaire avec sa rotation) (bug d’Havok1).
Lorsque je lie deux prims, la distance max ne correspond pas à la formule
Attention lors de votre calcul de ne pas confondre la distance entre les centres et la distance max de liaison entre les sphères de délimitation.