Interpolation/Cosine
< Interpolation
Jump to navigation
Jump to search
Revision as of 12:50, 4 September 2011 by Nexii Malthus (talk | contribs)
| LSL Portal | Functions | Events | Types | Operators | Constants | Flow Control | Script Library | Categorized Library | Tutorials | Interpolation |
Cosine Interpolation
Float Cosine | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
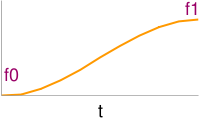
Cosine interpolation of f0 and f1 with fraction t. <lsl> float fCos(float f0,float f1,float t) { float F = (1 - llCos(t*PI))/2; return f0*(1-F)+f1*F; } </lsl>
Released to Public Domain. By Nexii Malthus
|
Vector Cosine | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Cosine interpolation of v0 and v1 with fraction t. <lsl> vector vCos(vector v0,vector v1,float t){ float F = (1 - llCos(t*PI))/2; return v0*(1-F)+v1*F;} </lsl>
Released to Public Domain. By Nexii Malthus
|
Rotation Cosine | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Spherical Cosine interpolation of r0 and r1 with fraction t. I liken to call it as SCORP <lsl> rotation rCos(rotation r0,rotation r1,float t){ // Spherical-Cosine Interpolation float f = (1 - llCos(t*PI))/2; float ang = llAngleBetween(r0, r1); if( ang > PI) ang -= TWO_PI; return r0 * llAxisAngle2Rot( llRot2Axis(r1/r0)*r0, ang*f);} </lsl>
Released to Public Domain. By Nexii Malthus
|
Rotation Cosine Aim | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Spherical Cosine interpolation of r0 and r1 with speed regulation. Does the entire animation loop to rotate between r0 to r1 up to peak speed, using the cosine interpolation it makes it appear to accelerate and decelerate realistically. <lsl> rCosAim( rotation r0, rotation r1, float speed ){ float ang = llAngleBetween(r0, r1) * RAD_TO_DEG;
if( ang > PI) ang -= TWO_PI;
float x; float y = (ang/speed)/0.2;
for( x = 0.0; x < y; x += 1.0 )
llSetRot( rCos( r0, r1, x/y ) );
} </lsl>
Released to Public Domain. By Nexii Malthus
| ||||||||||||||||||